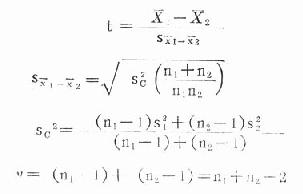|
《预防医学》 > 第十九章 计量数据分析
第三节 u检验和t检验u检验和t检验可用于样本均数与总体均数的比较以及两样本均数的比较。理论上要求样本来自正态分布总体。但在实用时,只要样本例数n较大,或n小但总体标准差σ已知时,就可应用u检验;n小且总体标准差σ未知时,可应用t检验,但要求样本来自正态分布总体。两样本均数比较时还要求两总体方差相等。
一、样本均数与总体均数比较比较的目的是推断样本所代表的未知总体均数μ与已知总体均数μ0有无差别。通常把理论值、标准值或经大量调查所得的稳定值作为μ0。根据样本例数n大小和总体标准差σ是否已知选用u检验或t 检验。 (一)u检验 用于σ已知或σ未知但n足够大[用样本标准差s作为σ的估计值,代入式(19.6)]时。
以算得的统计量u,按表19-3所示关系作判断。 表19-3 u值、P值与统计结论
例19.3根据大量调查,已知健康成年男子脉搏均数为72次/分,标准差为6.0次/分。某医生在山区随机抽查25名健康成年男子,求得其脉搏均数为74.2次/分,能否据此认为山区成年男子的脉搏高于一般? 据题意,可把大量调查所得的均数72次/分与标准差6.0次/分看作为总体均数μ0和总体标准差σ,样本均数x为74.2次/分,样本例数n为25。 H0: μ=μ0 H1: μ>μ0 α=0.05(单侧检验)
算得的统计量u=1.833>1.645,P<0.05,按α=0.05检验水准拒绝H0,可认为该山区健康成年男子的脉搏高于一般。 (二)t检验 用于σ未知且n较小时。
公式(19.7) 以算得的统计量t,按表19-4所示关系作判断。 表19-4 |t|值、P值与统计结论
例19.4 若例19.3中总体标准差σ未知,但样本标准差已求出,s=6.5次/分,余数据同例19.3。 据题意,与例19.3不同之处在于σ未知,可用t检验。 H0: μ=μ0 H1: μ>μ0 α=0.05(单侧检验)
本例自由度v=25-1=24,查t界值表(单侧)(附表19-1)得t0.05(24)=1.711。算得的统计量t=1.692<1.711,P>0.05,按α=0.05检验水准不拒绝H0,尚不能认为该山区成年男子的脉搏高于一般。
二、配对资料的比较在医学研究中,常用配对设计。配对设计主要有四种情况:①同一受试对象处理前后的数据;②同一受试对象两个部位的数据;③同一样品用两种方法(仪器等)检验的结果;④配对的两个受试对象分别接受两种处理后的数据。情况①的目的是推断其处理有无作用;情况②、③、④的目的是推断两种处理(方法等)的结果有无差别。
式中,0为差数年总体均数,因为假设处理前后或两法无差别,则其差数的均数应为0,d为一组成对数据之差d(简称差数)的均数,其计算公式同式(18.1);Sd为差数均数的标准误,sd为差数年的标准差,计算公式同式(18.3);n为对子数。 因计算的统计量是t,按表19-4所示关系作判断。 例19.5 应用某药治疗9例高血压病人,治疗前后舒张压如表19-5,试问用药前后舒张压有无变化? 表19-5 高血压病人用某药治疗前后的舒张压(kPa)
H0:该药治疗前后的舒张压无变化,即μd=0 H1:该药治疗前后的舒张压有变化,即μd≠0 α=0.05
自由度v=n-1=8,查t界值表得t0.05(8)=2.306,t0。01(8)=3.355,本例t=3.714>t0.01(8),P<0.01,按α=0.05检验水准拒绝H0,接受H1,可认为治疗前后舒张压有变化,即该药有降压作用。
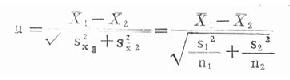
三、完全随机设计的两样本均数的比较亦称成组比较。目的是推断两样本各自代表的总体均数μ1与μ2是否相等。根据样本含量n的大小,分u检验与t检验。 (一)u检验 可用于两样本含量n1、n2、均足够大时,如均大于50或100。
算得的统计量为u 值,按表19-3所示关系作出判断。 例19.6某地抽样调查了部分健康成人红细胞数,其中男性360人,均数为4.660×1012/L,标准差为0.575×1012/L;女性255人,均数为4.178×1012/L,标准差为0.291×1012/L,试问该地男、女红细胞数的均数有无差别? H0: μ=μ0 H1: μ≠μ0 α=0.05 今x1=4.660×1012/L,s1=0.575×1012/L,n1=360; x2=4.1781012/L,s2=0。2911012/L,n2=255.
算得的u=13.63>2.58,P<0.01,按 α=0.05检验水准拒绝H0,接受H1,可认为该地男女红细胞数的均数不同,男性高于女性。 (二)t检验 可用于两样本含量n1、n2较小时,且要求两总体方差相等,即方差齐(homoscedasticity)。若被检验的两样本方差相差较大且差别有统计学意义则需用t'检验。
公式(19.10) 公式(19.11) 公式(19.12) 式中sx1-x2,为两样本均数之差的标准误,s2c为合并估计方差(combined estimate variance)。算得的统计量为t,按表19-4所示关系作出判断。 例19.7某医生统广西瑶族和侗族正常妇女骨盆X线测量资料各50例。骨盆入口前后径:瑶族的均数为12.002(cm),标准差0.948(cm),侗族相应的为11.456(cm)和1.215(cm)。问两族妇女的骨盆入口前后径是否有差别? H0: μ1=μ2 H1: μ1≠μ2 α=0.05 已知n1=n2=50,x1=12.002(cm),s1=0.948(cm); x2=11.456(cm),s2=1.215(cm).
本例自由度v=n1+n2-2=98,查t界值表[表内自由度一栏无98,可用内插法(从略)或用v =100估计]。T0.05(100)=1.948,t0.01(100)=2.626,今t=2.505>t0.05(1000,P<0.05,按α=0.05检验水准拒绝H0,接受H1,可认为广西瑶族和侗族妇女骨盆入口前后径不同,前者大于后者。
四、完全随机设计的两样本几何均数比较医学上有些资料为等比资料或正态分布资料,宜用几何均数表示其平均水平。比较两样本几何均数的目的是推断它们分别代表的总体几何均数是否相等。此种情况下,应先把原始数据X进行对数变换,用变换后的数据代入式(19.10)、(19.11)、(19.12)计算t值。 例19.8 将20名钩端螺旋体病人的血清随机分为两组,分别用标准株或水生株作凝溶试验,测得稀释倍数如下,问两组的平均效价有无差别? X1:标准株(11人)100,200,400,400,400,400,800,1600,1600,1600,3200 X2:水生珠(9人)100,100,100,200,200,200,200,400,400 H0: μ1=μ2 H1: μ1≠μ2 α=0.05 将两组数据分别取对数,以对数作为新变量X1和X2。 X1:2.000,2.301,2.602,2.602,2.602,2.602,2.903,3.204,3.204,3.204,3.505 X2:2.000,2.000,2.000,2.301,2.301,2.301,2.301,2.602,2.602 用变换后的数据计算 x1,s12;x2,s22再代入式(19.10)、(19.11)、(19.12)计算t值。 x1=2.794,s12=0.2043;x2=2.268,s22=0.0554
自由度v=11+9-2=18,查t界值表得t0.01(18)=2.878,今t=3.150>2.878,P<0.01,按α=0.05检验水准拒绝H0,接受H1,可认为两组平均效价不同,标准株高于水生株。
…… 第三节 正态分布和医学正常值范围的估计 附表18-1 标准正态分布曲线下的面积 第十九章 计量数据分析 第一节 均数的抽样误差和总体均数的估计 第二节 假设检验的基本步骤 第三节 u检验和t检验(当前页) 第四节 方差分析 第五节 假设检验中的两类错误及注意事项 第二十章 计数资料分析 第一节 相对数的常用指标 …… |
 公式(19.6)
公式(19.6)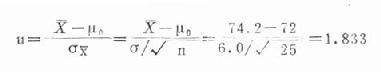


 公式(19.8)
公式(19.8)

 公式(19.9)
公式(19.9)