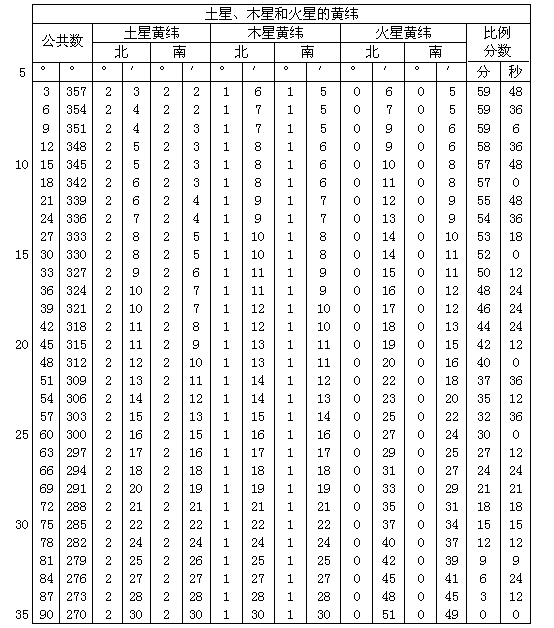
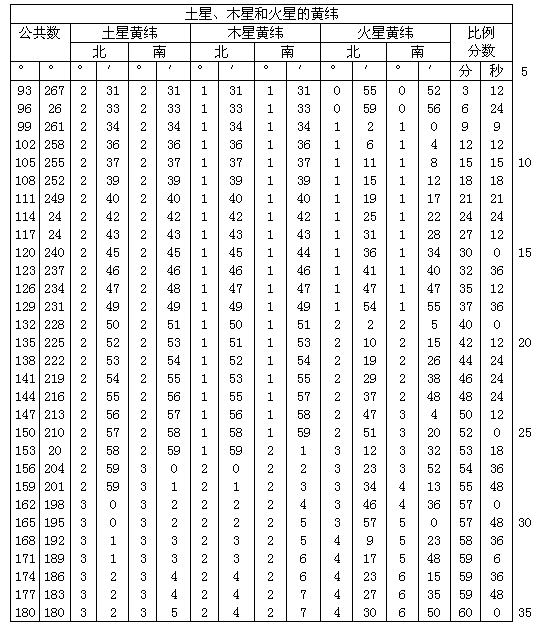
在对以上课题逐一进行阐述之后,还应谈到第三种纬度运动,即偏离。古人把地球置于宇宙之中心,认为偏离是由偏心圆的振动造成的,这与绕地心的本轮的振动有相同位相,其极大出现在当本轮位于[偏心圆的]远地点或近地点时[托勒密,《大成》,Ⅷ,1]。我在前面谈过,金星的偏离总是在北面1/6°,但水星为偏南3/4°(32)。
可是古人是否认为圆周的这个倾角是固定不变的,这还不完全清楚。他们认定总应取1/6的比例分数为金星的偏离,而3/4是水星的偏离[托勒密,《大成》,Ⅷ,6],这些数值表明了这一不变性。但这些分数值并不属实,除非倾角永远不变,而这是以此角为依据的比例分数的分布所需要的。进一步说,纵使倾角固定不变,仍然无法理解为什么行星的这一纬度会突然从交点恢复它原来的数值。你会说这一恢复就像(在光学中)光线的反射那样出现的。然而我们在这里讨论的运动并非瞬时的(33),而按其本质来说要求一个可以测定的(34)时刻。
图6—9
因此应当承认,这些行星具有我已经阐明的天平动[Ⅵ,2]。这种运动可使圆周的各部分[从一个纬度]变为反号的纬度。它也是它们的数值变化(对水星而言为1/5°)的一个重要结果。因此,如果按我的假设这个纬度在变化,并非绝对常数,这不应令人感到惊异。然而它不会引起可以察觉的不规则性,而这种不规则性在黄纬的各种变化中可以区分出来。
令水平面垂直于黄道。在[此两平面的]交线[AEBC]上,令A=地球中心,而在距地球为最大或最小距离处令B=实际上通过倾斜轨道两极的圆周CDF之中心。当轨道中心位于远地点或近地点,即在AB线上时,无论行星是在与轨道平行的圆周上任何地方,它的偏离为最大。这个[与轨道]平行的圆周的直径DF,与轨道的直径CBE相平行。此两[平行]圆周垂直于CDF平面,并可取[DF和CBE]两直径为[与CDF的]交线。平分DF于G,此点为[与轨道]平行的圆周之中心。连结BG、AG、AD与AF。和在金星最大偏离时一样,取角BAG=1/6°。于是在三角形ABG中,B为直角,可知两边之比AB∶BG=10,000p∶29p(35)。但在同样单位中整个 ABC=17,193p[CB=CA-BA=17,193p-10,000p=7,193p,CE=2×7193p=14,386p],而AE=[从AC=17,193p减去CE=14,386p的]余量=2807p。两倍CD或EF所对弦之半=BG。因此角CAD=6′,而EAF≌15′。前者与BAG[=10′]相差仅4′,后者为5′。这些数量很小,因此一般可以忽略。于是当地球位于远地点或近地点时,无论行星是在它的轨道上哪一部分,金星的视偏离度都只比10′略大或略小。
然而对水星而言,我们取角BAG=3/4°AB∶BG=10,000p∶131p(36),ABC=13,573p,而余量AE=6427p[=AB-BE=10,000p-3573p]。于是角CAD=33′,而EAF≌70′。因此前者短少12′[=45′-33′],而后者多余25′[=70′-45′]。然而在我们能够看见水星之前,这些差值实际上都被太阳的光芒淹没了。因此古人只研究过水星可察觉的偏差,而它似乎是固定不变的。
[早期版本:
然而,如果有人还想研究隐藏在阳光中的水星偏离,他[为此]耗费的精力会比前面提到的任何纬度都多。因此让我放弃这一课题并采用与真实情况相差不多的古人计算结果,否则在这一件小事上我(正如俗话所说)似乎是在和傻瓜的影子作斗争。可以认为上述论证对五颗行星的纬度偏离已经足够,对此我作了一个与前面的表[在Ⅴ,33之后]相似的30行的表。
[印刷版本:
然而,如果有人不畏辛苦想对为太阳所淹没的偏离取得可靠的认识,我在下面阐述如何做到这一点。
图6—10
我取水星为例,因为它的偏差大于金星。令直线AB是在行星轨道与黄道的交线上。令地球位于A,即行星轨道的远地点或近地点。和我对倾角的做法一样[Ⅵ,7],取直线AB=10,000p,此为在极大值与极小值之间没有任何变化的长度。以C为心画圆DEF,此圆在距离CB处与偏心轨道相平行。设想此时行星在此平行圆周上正呈现其最大偏离。令此圆的直径为DCF,它也应当平行于AB,而两条线都在与行星轨道垂直的同一平面上。举例而言,取EF=45°,我们研究行星在此弧段的偏离。作EG垂直于CF,并作EK和GH垂直于轨道的水平面。连结HK,完成矩形。还连结AE、AK及EC。
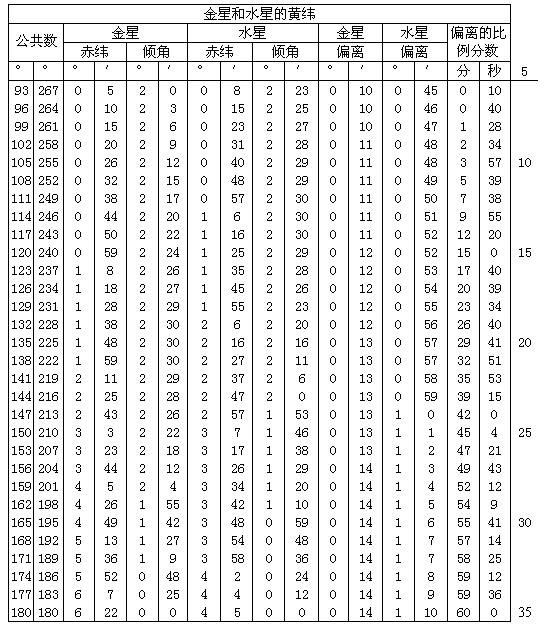
根据水星的最大偏离,在取AB=10,000p和CE=3573p时,BC=131p。在直角三角形[CEG]中,各角已知,边EG=KH=2526p。[从AB=10,000p]减去BH=EG=CG[=2526p],则余量AH=7474p。因此在三角形AHK中,夹出直角的两边已知[=7474p,2526p],故斜边AK=7889p。但是已取[KE=]CB=GH=131p。于是在三角形AKE中,形成直角K的两边AK和KE已知,角KAE可知。此即为对所采用弧段EF我们要求的偏离,它与观测相差很少。对[水星的]其他偏离以及对金星进行计算,我把所得结果列入附表。
图6—11
在作了上述解释之后,我对金星和水星在这些极限之间的偏离采用六十分之几或比例分数。令圆ABC为金星或水星的偏心轨道。令A与C为该纬度上的交点。令B为最大偏离的极限。以B为心画小圆DFG,其横向直径为DBF。令偏离的天平动沿DBF出现。假设当地球位于行星偏心轨道的远地点或近地点时,行星在F点呈现其最大偏离,而行星的均轮与小圆在该点相切。现在令地球位于离行星偏心圆的远地点或近地点任何距离处。根据这一行度取FG为小圆上的相似弧段。画行星均轮AGC。AGC与小圆相交并与在直径DF上截出E点。置行星于AGC上面的K点,而按假设弧EK与FG相似。作KL垂直于圆周ABC。需要由FG、EK和BE求KL=行星与圆ABC的距离。从弧段FG能够求得EG,可以认为它是一条与圆弧或凸线几乎一样的直线。同样,可求得用与整个BF或[从BF减去EF的]余量BE相同的单位表示的EF长度。BF∶BE=两倍CE象限所对之弦∶两倍CK所对之弦=BE∶KL。因此,如果把BF和半径CE都与同一数目60相比,由此可得BE之值。求它的平方并除以60,便得KL=所求弧EK的比例分数。我把这些分数列入下表的第五栏即最后一栏。