(1)哥白尼的手稿原来在对开纸142r第12行结束第五卷的引言，并立即转入第一章。他在写出该章标题和前面两句话后，勾掉这九行字并继续写引言，其目的是重用据说柏拉图在《蒂迈欧篇》中使用过的行星名称。然而柏拉图在《蒂迈欧篇》中并没有用这些名字来称呼五颗行星。这些名字是在他死后很久才出现的。
怎样解释这种误传呢？查耳西蒂斯（Chalcidius）的《柏拉图〈蒂迈欧篇〉注释》（Commentary on Plato’sTimaeus，巴黎1520年第一版）列出哥白尼重复使用的行星名称。如果查氏著作为哥白尼本段论述的依据，则可得出下列三项有趣的推论。
首先，哥白尼没有把查耳西蒂斯对《蒂迈欧篇》的评注与七个多世纪之前柏拉图本人在《蒂迈欧篇》中的论述区分开来。换句话说，哥白尼并未查阅《蒂迈欧篇》原书来考证柏拉图是否确实使用过这些行星名称。其次，哥白尼了解，不能认为大部份读者都通晓希腊文，因此对他们来说这些名称是陌生的，甚至是无法理解的。于是哥白尼并不算纯重引原名，还对这些行星名称的含义加以解释。他对金星加上两个人们很熟悉的名称。最后，如果查氏著作是哥白尼此处所用资料的根据，我们就更有理由认为他在1520年以后才开始写第五卷。实际情况是，当哥白尼在克拉科夫求学时，该处就有几部查氏的手稿。但是在他只有十几二十岁的时候，他能够有机会研读珍藏的手稿吗？这里所谈的行星名称也出现在其他一些古代作者（例如西塞罗·假普鲁塔尔赫·马丁纳斯·卡佩拉）的著作中，这也是事实。哥白尼了解这些著作，其中没有一部把这些行星名称与柏拉图的《蒂迈欧篇》联系起来。在另一方面，无论是在《蒂迈欧篇》还是哥白尼的著作中都出现这些行星名称。
(2)一颗行星“总是按其自身运动向前进”。然而它有时似乎停留和往反方向运动。这些偏离行星本身运动的现象不是真实的，而只是表观的。这些现象是由我们作为观测者在地球上绕太阳运动造成的。一位（假想的）观测者在（可认为是静止不动的）太阳上观看，行星就只作其固有的、向前的运动。他看不到停留和方向改变。这个见解是哥白尼对我们了解行星状态最杰出的贡献。它同时还为地球绕太阳的周年运转提供一个鲜明的证据。人们常说，对这种运转的第一次证明是用大为改进的望远镜察觉由恒星周年视差显示的地球周年运动对恒星产生的效应，而这在哥白尼时代是办不到的。但是他所发现的行星视差（他称之为行星的“交替运动”（motus commutationis），即往返运动），对地球的轨道运动而言是和恒星周年视差同样有力的证据。在技术条件成熟之后才发现该现象的详细情况。但是作为一种大尺度现象，行星视差是哥白尼用肉眼发现的。参阅让·克洛德·佩克尔（Jean-Claude Pecker）著“哥白尼、开普勒、贝塞耳论往复运动及其视差”（Retour sur Copernic，Kepler，Besselet les parallaxes），载《天文学》（L’Astronomie），1974，88．
(3) 此处也像第二卷引言中的情况，哥白尼提醒读者，使用通常的日动论术语有时很方便，并且没有害处[参阅第二卷注释(3)]。
(4) 哥白尼由于重写错误写成“六倍”（sexies），而应为“六十倍”（sexagies；对开纸143r倒数第13行）。这大概是由于他已经想到在三行下面要提到的木星的六个恒星周。
(5)在金星逐日行度的第二栏，哥白尼由于笔误写上49（iL，对开纸143r倒数第14行）。但按附表（对开纸147v第3行）以及为与金星周年行度相协调，此数应为59。
(6) 西塞罗在他的Republic第六卷中加入一节，题为“西比奥之梦”。此节读到行星“沿其圆周和球形”途径运行（§15）。
(7) “一个圆周运动对于其自己以外的其他中心也能是均匀的”，承认此点是使哥白尼“得以考虑地球运动、保持均匀运动的其他方式以及科学原理”的条件之一。他对此仍然不愿采用“载轮”一词来建立地球是一个运动天体的概念。然而他的早期著作《要释》确曾提到“某些载轮”（aequantes quosdamcircu-los），这促使他设法找到“一个更合理的安排，以便按绝对运动规律的要求，每个物体都绕其自身的中心作均匀运动”（3CT第57—58页）。
在哥白尼之前五百年，伟大的穆斯林科学家伊本·阿耳·海沙姆（IbnAl-Haytham，965—1040年）也扬弃了载轮，因为它违反均匀运动的原则。他在自己的著作《有关托勒密的疑点》（Doubts concerning Ptolemy）中便是这样做的。此书的阿拉伯文译本最近出版（Al-Shukuk'alaBatlamyus，开罗国家图书馆出版社1971年版），但从未译为拉丁文，因此哥白尼不会读到它。然而哥白尼是否听到过关于伊本·阿耳·海沙姆反对载轮的轻微的传说呢？如果是这样，值得注意的是那位穆斯林学者摒弃载轮并未使他想到地动学说。参阅沙罗蒙·派恩斯（Salomon Pines）著“伊本·阿耳·海沙姆评托勒密”（Tbn Al-Haytham'sCritique of Ptolemy），《第十届国际科学史会议文集》（巴黎1964年版，第548—549）页。
(8)哥白尼认为，古代天文学家相信行星偏离绝对的圆形轨道。说他认为他们的行星轨道为绝对圆形以及他想要“驳斥古人的见解”，这些错误概念都来自印刷版本，而这些版本都没有印出对开纸151r第7行的冒号。因此它们弄错了哥白尼的意思。奥托·纽格保尔（Otto Neugebauer）“论哥白尼的行星理论”（On the planetary Theory of Copernicus），《天文学展望》（Vistas in Astronomy），10∶94）对此点当然会是清楚的。因此如果他不是只根据印刷版本而查阅过原稿，他就不应该指责哥白尼犯了一个严重的错误。
(9)哥白尼在分析五颗行星的黄经行度时，从土星开始，接着依次为两颗外行星，即木星与火星，然后是金星和水星。托勒密却按相反次序，从水星向外至土星（PS，Ⅸ，7—Ⅺ，8）。然而在他的表中（PS，Ⅸ，4；Ⅺ， 11； Ⅻ，8）以及在处理逆行弧长时（Ⅻ，2—6），托勒密却转而采用哥白尼的次序。
(10)PS1515（对开纸122v）把这个埃及月份的名称篡改为“machur”，这被哥白尼解释成Mechyr（对开纸152r第4行），即埃及历六月份，而托勒密却认为这是九月份（Pachon）。梅斯特林以外的某人在其N抄本中（对开纸143r右边缘），第谷在其B抄本中以及A首次公开地，都做了这项改正。
(11)托勒密对第一次冲得出土星的经度为天秤宫内1°13′，即181°13′。对此数作大约6°33′的岁差改正，哥白尼得约数（fere）为174°40′。在另一方面，他对第二次和第三次冲所作的岁差改正量为精确值6°37′。那么他对第一次冲为什么作近似改正？这肯定不是像Z（第510页）所设想的那样是一个“计算错误”。Z没有注意到，哥白尼注明在第一次冲时土星的位置只是近似的。
(12)哥白尼由于笔误写上undecim（11），而应为quindecim（15），但在三行之下他正确地写出罗马数字xv。第谷在其B抄本中把11改为15（对开纸143v第4行）。
(13)托勒密取土星在第二次冲时的位置为人马宫内9°40′，即249°40′。因此，哥白尼在这次所取的岁差改正值为精确值6°37′+243°3′=249°40′。
(14) 托勒密取土星在第三次冲时位置为摩羯宫内14°14′，即284°14′。哥白尼又一次采用准确的岁差改正值6°37′+277°37′=284°14′。
(15) 从127年3月26日5P. M.至133年6月3日3P.M.∶
127年3月 5d 7h
4月至12月 275
5个整年（128—132年）
133年 1月至 5月 151
6月 2 15
闰日（128—132年） 2
──
435
1 -365
── ────
6y 70d22h=55dm
(16) 按Ⅴ、1后面的土星逐年和逐日视差行度表
对6y 为240°
45 12′18″58″″
70d∶60d 57 7 44 5
10 9 31 17 20
22h≌ 52
────────────────────
6y70d 22h 352°43′20″23″′，哥白尼把后一数字写为352° 44′。
(17)从133年6月3日3P. M.至 136年7月8日11P.M.：
133年6月 27d 9h
7月至12月 184
2个整年（134—135年）
136年 1月至 6月 181
7月 7 11
闰日（136年） 1
────
400
1 -365
── ────
3y 35d20h（=50dm）
(18)按Ⅴ，1后面的土星逐年和逐日视差行度表，
对3y 为300°
22 36′
35d 33 19
20h≌ 48
──────────────────
3y35d20h 356°43′
(19) 哥白尼的证明要求把A、B和C都与E相联。但他的证明并不使用AE，BE，CE与小本轮圆周的交点，因此哥白尼在他的图中（对开纸152v）没有给这些交点以符号。K，L和M为小本轮圆周的交点，K，L和M为小本轮圆周与 AD、BD和 CD的交点，而非与AE、BE和CE的交点。
(20) 阿基米德对求面积（几乎）等于圆面积的正方形的问题进行了间接的攻击。参阅第三卷注释（132）。
(21)有人指责哥白尼只会鹦鹉学舌式地追随托勒密。这些人应当仔细考虑哥白尼在此摒弃了托勒密过份繁琐的论述。
(22) 实际上托勒密的第一弧段=57°5′（PS1515，对开纸124v）。托勒密对第二弧段得出18°38′（而非对开纸153r第9—10行的18°37′）。
(23) DF∶DE=60p∶6p50′=10，000∶1139。哥白尼由于一个奇怪的笔误把1139写1016（对开纸153r第12行），他似乎取DE=6p5′45″36′″。但就在下面一行，他实际上是用1139作计算，因为他取此处所谈的数目的3/4等于854，并取它的1/4等于285。梅斯特林在其N抄本中和第谷在其B抄本中（对开纸144r倒数第3行）都把1016改为1139，但第一次公开作这个改正的是A。
(24) 哥白尼原来取 BDE=161°23′（对开纸153r倒数第4—3行）。因此他当时还是用FB=18°37′作计算[见上面注释（22）]。后来他擦掉第一个i，把BDE的分数改为22。他这样做，便回到托勒密对第二弧段所取的数值18°38′。
(25)哥白尼由于笔误把OBL的分数写为36（对开纸153v第2行）。但是他实际上是用38在作运算（见上一条注释）。
(26)哥白尼把BED误认为余量（对开纸153v第6行），但Mu（第298页第31行）首先指出，它应为被减量。
(27) 哥白尼误取角CDE等于56°30′，实际上应为此角的补角。1952年的英译本（第747页）首先指出这一错误。哥白尼原来把分数写成30（xxx；对开纸153v第9行）。他在此行上面和最后的x之前插入一个i，于是把该数减为29。然而他实际上还是用30′（第247页第2行）进行运算，并在v、5接近末尾处（对开纸154r第18行）用分数1/2的开式再次使用这个数字。
(28) 哥白尼由于预想重写错误把分数37写成14，因为他已经想到在本行末尾的14（对开纸153v倒数第2行）。梅斯特林的N抄本（对开纸145r第4行）改正了这个错误。
(29) 哥白尼由于笔误把应有的 PEF写为PDF（对开纸153v末行）。梅斯特林的N抄本（对开纸145r第5行）改正了这个错误，而Mu（第299页第12行）首次作公开的更正。
(30)哥白尼原来认为这次冲的时刻为“午夜后几乎9h”（对开纸154v倒数第2行）。接着哥白尼把数目字擦掉（现在它已难以认出），并在右边缘改写出“日出前2h”。最后，他把这个第二说法改为“午夜后62/5h”，并在对开纸156v倒数第7—6行重复一遍。于是他从头至尾由“几乎9”改为4，再改为6∶24，而这三个时刻都是在清晨前后。把这次冲说成是在黄昏，这是一个惊人的错误。Z（第209页）论证说哥白尼不可能用月亮（当时为新月）作为媒介，并说哥白尼把这次冲完全弄错了。Z认为应当把这次冲推迟一个月到11月10日！但是哥白尼是在五行之下[对开纸154v第4行；参阅下面的注释（32）]计算第二次与第三次冲的时间间距之前采用最后时刻（6∶24 A.M.）的。该时间间距当然与Z的强词夺理的批评完全不符。
(31)从1514年5月5日10∶48 P.M.至1520年7月13日正午：
1514年5月 26d1h12m
6月至 12月 214
5个整年（1515—1519年）
1520年 1月至 6月 181
7月 12 12
闰日（1516和 1520年） 2
────
435
1 -365
── ────
6y 70d13h12m=33dm
(32)从1520年7月13日正午至1527年10月10日6∶24 A.M.∶
1520年 5月 18d12h
8月至 12月 153
6个整年（1521—1526年）
1527年 1月至 9月 273
10月 9 6 24m
闰日（1526年） 1
──
454
1 -365
── ────
7y 89d18h24m=46dm
(33)前面已经谈到（Ⅴ，1），哥白尼认为不需要为土星的平均自行度造表。他对土星自行度取1y为12°12′46″，因此6y为73°16′36″。从Ⅲ，14末尾的太阳逐年和逐日简单均匀行度表内有关栏目减去Ⅴ，1末尾的土星逐年和逐日视差行度表的某些栏目，可得其余的土星自行度。于是对70d33dm有
60d 太阳 59°8′ 土星 57°7′
10 9 51 9 31
── ──── ────
70d 68°59′ 66°38′
-6638
────
2°21′
33dm≌ 1
────
2°22′
6y 73 16 36″
────
75°38′36″，哥白尼把此数写为
75°39′。
(34)DE∶AE=19090∶8542=13501∶6041。哥白尼把6041写成6043（对开纸154v末行）。他这样做是因为他原来取DE=13506（对开纸154v倒数第12行，他在该处擦掉6并在它上面写1，而在倒数第2行6仍比1明显）。取DE=13506，则AE=6043。当哥白尼把DE从13506改为13501时，他忘记对AE作相应改变，它仍然=6043。
(35)对开纸155r倒数第16行：哥白尼在做此减法时，把减数与被减数巅倒了。W首先改正这一错误。
(36)FG∶FD=10，000∶1200=60p∶7p12′。
(37)FD∶DK=1200∶650=10，000∶54162/3。最后一位数被擦掉一部份，但不是7，看起来像1（对开纸155r倒数第7行）。按弦长表，对32°50′为54220，对 32°40′为 53975，因此对 32°45′为 54098，而取半径=10，000时为5410。与54167相应的角度约为32°48′。
(38)哥白尼原来写的是7（vij；对开纸154r末行）。然而他在此处说的是8（octo；对开纸156v第12行）。如果他在此处保留7，则土星的低拱点会在601/3°，而不需要用“约在”（fere；对开纸156v第16行）。但他在Ⅴ，6末尾取土星高拱点在 240°21′（对开纸156v倒数第3行）时，他肯定是取8。
(39)哥白尼原先取这次观测的时间为“日出前2h（=4 A.M.，对开纸157r第11行）。后来他取较晚的时刻，把2换成6，没有分数，并且不像前面[见注解（30）]那样把“日出前”改成“午夜后”。
(40)从136年7月8日11A.M.至1527年10月10日6 A.M.：
136年 7月 23d13h
8月至12月 153
1390个整年（137—1526年）
1527年1月至9月 273
10月 9 6
闰日（140—1524年） 347
──
805
2 -730
── ────
1392y 75d19h=471/2dm
哥白尼写的是48dm ，这也许是因为他想起自己对第三次冲最后确定的时刻为6点以后几分钟。
(41)哥白尼在此处（对开纸157r第20行）所写分数为45。这与他在六行之上原来的计算结果相符。然而他在该处插进三个i，使分数增为48。但他是在用手稿中未经改正的较小数目作减法之后才把45改为48。哥白尼在修改数字结果后在其他地方不作相应的变化，此处又是一例。
(42)相应的现代数值应为每100年11/2′（《天文学杂志》，1974，79∶58）。
(43)从基督纪元开始至哈德里安20年12月24日=136年7月8日：
135个整年
136年 1月至 6月 181d
7月 7 11h
闰日（4—136年） 34
── ────
135y 222d11h=271/2dm，哥白尼将此数写为27dm（对开线157r倒数第5行）。
(44)从基督纪元开始至1514年2月24日5A.M.：
1513个整年
1514年1年 31d
2月 23 5
闰日（4—1512年） 378
──
432
1 -365
── ────
1514y 67d5h=121/2dm ，哥白尼把此数写
为13dm（对开纸157v倒数4—3行）。哥白尼在该处的错误值77d（1xxvij，多出一个x）已在A中（第355页）改正。
(45)此处哥白尼取土星的高拱点在“大约2401/3”处（fere；对开纸158r第3行）。哥白尼在Ⅴ、6末尾更确切地说为在“240°21′”（对开纸156v倒数第3行）。
(46)哥白尼由于笔误（对开纸158r第17行）把应为41的度数写成40（xl，缺一个i）。A（第355页）改正了这个错误。
(47)虽然哥白尼在上面（对开纸158r第1行）已经取分数为31，他在此处由于笔误写成33。A改正了这个错误。
(48)哥白尼把应该写在上面一行的数字（31′）写在这里。他没有注意此处需要的数字（35′）。也是A改正了这个错误。哥白尼显然没有像他把计算结果从演算纸抄到手稿上那样仔细。
(49)BD∶EL=10，000∶1090=60p∶6p322/5′，哥白尼把后一数字写为32′（对开纸158v第8行）。
(50)按托勒密的土星理论，本轮的半径（与哥白尼理论中的地球周年运行轨道的半径相似）=6p30′（PS，Ⅺ，6）。
(51)1090∶ 10，569=1p∶9p41.8'，哥白尼把后一数字写成42′（对开纸158v第 16行）。
(52)1090∶9431=1p∶8p39′。
(53)哥白尼由于笔误（对开纸159r第3行）把度数写为6（vj）。A（第357页）改正了这个错误。
(54)从哈德里安 17年11月 1日 11P.M.至哈德里安21年2月 14日 10P.M.：
哈德里安17年11月 28d13h
12月 30
闰日 5
3个整年（哈德里安18—20年）
哈德里安21年1月 30
2月 13 10
────────────────────
3y 106d23h
(55)从哈德里安 21年 2月 14日 10 P.M.至皮厄斯·安东尼厄斯 1年 3月 21日 5 A.M.：
哈德里安21年2月 16d14h
10个整月（3月至12月） 300
闰日 5
皮厄斯·安东尼厄斯1年
2个整月（1月和2月） 60
3月 20 17
──
1 7h
──
402
1y -365
──
37d
(56)60p：51/2p=10，000：9162/3p，哥白尼把后一数字写为917（对开纸159r倒数第9行）。
(57)哥白尼由于笔误（对开纸159v第10—11行）把EAD和DEA弄巅倒了。W（第371页）改正了这个错误。
(58)哥白尼为简便计省略了他在几何推理中的一些步骤。因此，如果把DB与EL的交点称为Y，则得
LEB+DBE（=4′+12′）=DYE=16′，和
FDB=177°10′=（DYE=16′）+（FEL=176°54′）。
(59)ECM=（DCE=2°8′）+DCM
由图，DCM=FDC
但是 FDC=180°（-GDC= 30°36′）= 149°24′
∴ECM= 2°8′+ 149°24′=151°32′，并非哥白尼所设想的（对开纸160r第7行，他在该处原有另一个数，但局部擦掉无法辨认）为147°44′。梅斯特林在其N抄本中（对开纸150v倒数第5行）把它改为151°32′，而W首先作公开改正。
(60)LEM=（GEM=33°23′）+（LEG=3°6′）=36°29′
LEG=180°-（FEL=176°54′）=3°6′
(61)哥白尼在此处由于笔误把分数写成30（xxx，对开纸160r第18行）。然而不久后他改用正确值22（xxij，对开纸160r倒数第4行）。梅斯特林在其N抄本中（对开纸151r第6行）把30换为正确值22，而W首先公开作这个改正。
(62)从1520年4月30日11A.M.至1526年11月28日3A.M.：
1520年 4月 13h
5月至12月 245d
5 个整年（1521—1525）
1526年 1月至 10月 304
11月 27 3
闰日（1524） 1
──
577
1 -365
── ────
6y 212d16h=40dm
(63)从1526年11月28日 3A.M.至1529年2月1日7P. M.：
1526年 11 月 2d21h
12月 31
2个整年（1527—1528年）
1529年 1月 31
2月 19
闰日（1528） 1
──
（24+）16h
1
──
2y 66d
此处哥白尼把16h写成39dm（对开纸160v第12行），而他在前两次冲之间把16h正确地取为与其对应值40dm相等。他是否原来把第三次冲的时刻定为1529年 2月 1日 6∶36P.M. 而不是7P. M.？
(
64) ED= 10918p（对开纸160v倒数第3行）应为与
CED相对边的正确长度。此角为内接角时=
66°10′，而为中心角时= 33°5′。按弦长表，对33°10′为54，708，对33°0′为54，464，因此对33°5′为54，586，而在取半径=
10，000时为5459。2×5459=10，918，此为哥白尼对ED误取的数值。如果他没有把66°10′=
CED与64°10′= 
DCE混为一谈，他就会得到与托勒密的结果很好相符的
ED值。安东尼·潘涅柯克（Antonie Pannekoek）首先公开指出哥白尼的错误“哥白尼《天体运行论》中一个值得注意之处”（A
Remarkable Place inCopernicus’Derevolutionibus），载《荷兰天文研究机构公报》（BulletinoftheAstronomi-cal
Institutes of the Netherlands，1945，10∶68—69）。第谷在他的B抄本中改正了哥白尼的错误及其后果（对开纸151v—152r）。
(65)ED∶AE=18992∶9420=10，918∶5415.3，哥白尼把后一数字写为5415（对开纸161r第9行）。
(66)CE∶DE=18150∶10918=17727∶10663.5，哥白尼原来把后一数字写成10663，但后来在3上面写了一个5（对开纸161r第17行）。
(67)哥白尼由于重写错误（对开纸161r倒数第14行）把ED×DB写成ED× DE。N（对开纸152r）改正了这个差错。
(68)哥白尼由于笔误把这个减法中的两项弄巅倒了，即写成从长方形GD×DH中减去（FDH）2（对开纸161r倒数第 11行）。T（第347页第 15—17行及注释）改正了这个错误。
(69)FG∶FD=10，000∶1193=60p∶7p9.48′，哥白尼把后一数字写为9′（对开纸161r倒数第8行）。
(70)然而哥白尼在Ⅴ，5中报导说托勒密求得的土星偏心距=6p50′=1139=854+285，而他在Ⅴ，6中把这个偏心距增大为7p12′1200=900+300，并说只是“稍微不同”（parum distant对开纸155r倒数第11行）。
(71)哥白尼在Ⅴ，10中报导说托勒密求得的木星偏心度=51/2p=917，“与观测几乎刚好相符”（observatis propemodum respondebant，对开纸159r倒数第8—7行）。此处在Ⅴ，11中，哥白尼自己对木星得出的偏心距=7p9′=1193。
(72)如果哥白尼对
DCE没有误取孤长[此即注释（64）所提到的错误]，他对木星偏心度所得数值就不会与托勒密的值相差很远。
(73)哥白尼由于笔误（对开纸162r第5行）把
EAK的分数写成34（xxxiiij）。梅斯特林在其N抄本中（对开纸152v倒数第5行）把这个数值改为41，而T（第349页第4行及注释）首次作公开改正。
(74)哥白尼在此处又一次为简便计略去几何推理中的几步。若令AD与KE的交点为X，则有
（AEK=57′）+（DAE=2°39′）180°-（AXE=176°24′）
但是AXE=（ADE=180°-45°2′=134°58′）+（KED=41°26′）。
(75)DEL=DEB-（BEL=1°10′）
但是DEB=180°-（BDE=64°42′）-（DBE=3°40′）=111°38′，因此DEL=111°38′-1°10′=110°28′。
(76)哥白尼由于笔误（对开纸162r倒数第12行）把这个角误称为AED。以前各版或译本均未察觉这个错误。
(77)哥白尼由于笔误（对开纸162r第6行）把此角误称为FCD，T（第349页第20行）悄悄改正了这个错误。
(78)哥白尼由于笔误（对开纸162r倒数第5行）把此边误称为DE。Mu（第315页第9行及注释）改正了这个错误。
(79)哥白尼在对开纸162r的图上没有给DC和EM的交点以任何符号。称此交点为X，则有
EXC=180°-（XEC=1°）-（DCE=2°51′）=176°9′。
但EXC=ECX（=180°-[FDX=49°8′]=130°52′）+（DEX=DEM），
因此176°9′=130°52′+DEM，并得
DEM=45°17′。
(80)哥白尼把
LEM的分数写为10（x，对开纸162v第5行）。原因是在他原来对
DEM所取的数值中分数为18（对开纸162v第3行）。他在用18做完减法并得出结果为10′后，他回到第3行并擦掉第三个i，但没有改正由减法得出的结果。
(81)木星的视差行度有1′的差错，这可能是由于哥白尼用对开纸162v左边缘的52′，而不是用相邻的第20行中的51′进行计算。属于视差的应为51′，而非52′。
(82)哥白尼把“约为”（fere，对开纸162v倒数第6行）一词放错了地方。它应与木星的视差行度1°5′，而不该与木星的平均行度104°54′在一起。
(83)托勒密的观测时间为5A.M.，而他自己是在7P.M.。哥白尼怎能由此得出差值为37dm（=14h48m），对开纸163r第1行）？要使其余时段=1392y99d，他应取托勒密观测的埃及历日期为137年10月7日：
137年 10月 24d
11月和12月 61
1391个整年（138—1528年）
1529年 1月 31
闰日 347
1（取自小时栏）
──
464
1 -365
── ────
1392y 99d
(84)相应的现代值应为每300年大约 11/2（《天文学杂志》，1974，79∶58）。
(85)按这种算法（对开纸163r第14行），托勒密的观测是在137年11月11日，而这个日期与Ⅴ，12的计算不能相容[参阅注释（83）]。哥白尼把小时数写为10dm=4h。他把它写在右边缘，用以代替原来用的数目5（对开纸159r第 6行，162v倒数第3行）。
(86)哥白尼指明为 3月 1日之前的第 12天（对开纸163r倒数第 4行）。他在对开纸163v第3行的计算表明，他没有考虑到1520年为闰年，即有2月29日。
(87)从基督纪元开端到1520年2月18日6A.M.：
1519个整年
1520年1月 31d
2月 17 6h
闰日（4—1516年） 379
──
427
1 -365
── ────
1520y 62d6h=15dm
(88)FE∶ES=9698∶1791=10373∶1915.7，哥白尼把后一数字写成1916（对开纸164r第13行）。
(89)60p∶11p30′=10，000∶19162/3。
(90)RET∶ADC=2×1916∶2×10，000=3832∶20，000=1p∶5p13′9″。哥白尼在对开纸164r第20行所写为后一数字，但此处在第18—19行他认为取5p13′已足够准确。
(91)AD∶DE=10，000∶687=5p13′∶21′30″，哥白尼把后一数字写为21′29″（对开纸164r倒数第15行）。然而这个差异可以忽略不计，因为他取BF=1/3 DE=7′10″（见同行）。但他在计算木星位于远日点与近日点的距离时，实际上是用BF=7′9″进行计算。
(92)从哈德里安15年5月26日1A.M.至哈德里安19年8月6日9P.M.：
哈德里安15年5月 3d11h
7个整月 210
闰日 5
3个整年（哈德里安16—18年）
哈德里安19年7个整月 210
8月 6 9
──
434
1 -365
── ────
4y 69d20h=50dm
(93)从哈德里安19年8月6日9P.M.至皮厄斯·安东厄纳斯2年11月12日10P.M.：
哈德里安19年8月 23d15h
4个整月 120
闰日 5
3个整年（哈德里安20—21年，
皮厄斯·安东尼厄斯1年）
皮厄斯·安东尼厄斯2年10个整月 300
11月 12 10
────
1(24+)1h
───
461
1 -365
── ────
4y 96d
(94)哥白尼在给出
ADE的大小时除138°外忘记提到分数（27′）。他指出
ADE=180°-（ 
FDA=41°33′），见对开纸164v倒数第3行。
(95)哥白尼由于笔误（对开纸165r第20行）把第二角误称为AED而非LED。T（第355页第32行及注释）改正了这个错误。随后在下面一行中，为了能自圆其说，哥白尼写上DEA，而书中要求的是DEL，T悄悄做了改正。如果把DA与EL的交点叫做X，则AEL+DAE=1°56′+5°7′=7°3′=DXE。但是DXE=7°3′=ADF-DEL=41°33′-34°30′。哥白尼后来对在火星第二次冲的讨论快结束时，为计算整个MEL而取DEL（并非DEA）=34°30′。在另一方面，DEA=DEL+AEL=34°30′+1°56′=36°26′。
(96)哥白尼由于笔误（对开纸165r倒数第8行）把
EBM的分数写为13（xiij），而此数应为9。
(97)哥白尼取 CED=37°39′（对开纸165v第 3行），这是一个重大错误。他显然是由减法CDE-DCE=44°21′-6°42′=37°39′而得出上列结果。其实他当然应该使用减法180°-（DCE+CDE=6°42′+44°21′=51°3′）=128°57′。然而他在紧接着下面的第7行求NED时，他不言而喻地用了CED=128°57′≠37°39′。梅斯特林在其N抄本中（对开纸156r倒数第4行）把37°39′改为128°57′。
(98)从1512年6月 5日1A.M.至1518年12月 12日 8P.M.历时6y191d。哥白尼把19h=471/2dm。写成45dm（=18h，对开纸166r第15行）。
(99)从1518年12月12日8P.M.至1523年2月22日5A.M.历时4y72d。哥白尼把9h=221/2dm写成23dm（对开纸166r第16行）。
(100)此图由 N（对开纸157v）提供，用以取代哥白尼在手稿中（对开纸166v）开始绘制但后来弃置不用的图。
(101)哥白尼由于笔误（对开纸166v第5行）把BF的分数写为18（xviij），但他在计算火星第二次冲时用的是25。
(102)哥白尼在对开纸166v左边缘插入对三角形BDE的讨论。他在该处把BDE的分数最后写为35（xxxv），这与前注中指出的BF的数值25相符。然而他没有改正第5行中的数值18。另一方面，他原来在边缘写的分数似为37，但应为42才能与BF的18相合。这些不一致之处不足为奇，因为哥白尼在图中除圆外只画了四条必需的线，他没有把图画完并给符号。
(103)哥白尼原来把EBM的分数写成18（xviij，对开纸166v末行），这似乎只不过是对BF所数值18（见前两条注释）的粗心的重复。然而他后来把18删掉并代之以36（xxxvj）。后一数目是他取BF的分数为25得出的。值得注意的是他没有把第 5行中的 18改为 25。
(104)如果令NE和CD的交点为X，则CEN+DCE=50′+2°6′=2°56′=DXE=FDC-DEN=16°36′-13°40′。
(105)哥白尼的数字每世纪约47′又是远大于现代值每世纪约27′（《天文学杂志》，1974，79∶58）。
( 106) 在把托勒密的第三次观测归化为克拉科夫地方时间时，为了将它与自己的观测相比较，哥白尼把亚历山大时间 10P. M. （ Ⅴ，15）改为克拉科夫时间9P. M. 。这是因为他假定克拉科夫是在亚历山大城之东1h= 15°（Ⅲ，18）。
( 107) 哥白尼（Ⅴ，18）认为这个埃及日期（皮厄斯·安东尼厄斯 2年 11月 12日 9P. M. ）等于 139年 5月 27日8 ∶ 48P. M.。 从此时至 1523年 2月 22日5A. M. 共历时1384y251d10h12m（251/2dm）。哥白尼把后一数字写为19dm（= 7h36m，对开纸168r第3行）。
(108) 从基督纪元开端至皮厄斯·安东尼厄斯 2年11月 12日9 P. M.，哥白尼算出历时138y180d52dm：
138 个整年
闰日（4—136年） 34d
公元139年1月至4月 120
5月 26 52dm（=8∶ 48 P.M.≌9 P.M.）
── ──
138y 180d，139年 5月 27日 9 P.M.（见前注）。
(109)哥白尼在对开纸168r右边缘把这个视差行度的分数最后写为22（xxij）。因为他在对基督纪元的开端算出位置=238°22′（见本章第 7行），此时他实际上用4作运算，所以哥白尼似乎是由于重写错误在本章第4行右边缘写上22。第谷在其B抄本中（对开纸158v第18章第5行）把22改成4，而W首先公开作此改正。
(110)火星
(111) FSE= 70°32′。按弦长表，对70°40′为94，361，对70°30′为94，264，因此对70°32′为94，283.4，或在取半径=10，000时为9428。
(112)EFS=35°9′。按弦长表，对35°10′为57，596，对35°0′为57，358，因此对35°9′为57，572.2，或在取半径=10，000时为5757。
(113)EF∶ES=9428∶5757=10，776∶6580.1，哥白尼把后一数字写成“约为6580”（fere，对开纸169r倒数第6行）。
把在 56上面的一个现在已经无法辨认的分数划掉（对开纸169v第4行），最后写上57″（1vjj）。
插入vj，对后一数字最终写出26″（对开纸169v 第 4行）。这个从 20″到 26″的变化与Ⅵ，3中删去的一段有关。哥白尼在该处擦去某个数字（大概是vj，对开纸193r第1行），而留下20。
(116)哥白尼（对开纸169v倒数第 6行）误认为这位西翁来自亚历大城。但是亚历山大的西翁生活于四世纪，即远在托勒密逝世之后。其观测资料供较为年轻的同时代人托勒密使用的，是另一位西翁。然而托勒密并未把这个西翁与斯穆尔纳或任何其他希腊团体联系在一起。托勒密曾说，他找不到对当代的需要适用的古代天文学家的观测资料。可是托勒密接着谈到：“在另一方面，我确实找到我对这项研究所需要的现代观测。我从数学家西翁的观测中找到了这样的资料…”（PS 1515，对开纸109r，第 1章第 11—14行）。托勒密提到他的同时代人“数学家”西翁，还说他得到了西翁的观测资料。这些情况也许使哥白尼得到一个错误印象，即这位西翁与亚历山大城有关。
哥白尼在1539年夏季收到列蒂加斯寄送的一册托勒密的《天文学大成》希腊文第一版（巴塞耳，1538年）。该书附有西翁的评论。封面用希腊文和拉丁文明显标出这位评论家是“亚历山大的西翁”。如果哥白尼在撰写v，20之前即便只是粗略看一下这张封面，他也会立该了解到为《天文学大成》写评论，因而出生迟于托勒密的这位亚历山大西翁，不可能是托勒密在世并撰写《大成》时借用其金星观测资料的那位西翁。因此我们可以认为，哥白尼是在写完v，20之后才看到西翁的评论。
在另一方面，哥白尼在撰写v，35（对开纸197v）时采用了他从《大成》1538年出版才能查出的一个词。因此我们确定哥白尼收到列蒂加斯赠送的、附有西翁评论的那本《大成》，是在写完v，20之后和撰写v，35之前。
(117)托勒密取平太阳在双鱼宫内141/4°，即344°15′。哥白尼从此数减去由岁差引起的6°34′，才能得出337°41′。
(118)哥白尼起先认为皮厄斯·安东尼厄斯4年即是公元144年，后来以为是公元142年（对开纸170v第5行）。这只是他的笔误。这可从他在《驳魏尔勒书》（3CT第94—97页）中的详细讨论看出。此外，他在Ⅴ，26中把皮厄斯·安东尼纳斯4年取为公元140年（对开纸176v末尾三行）。梅斯特林在其N抄本中（对开纸160v第5行）把此处Ⅴ，20中的错误年份142改为140，而Me第56页注释）首先对此作公开的改正。
(119)托勒密取平太阳在狮子宫内53/4°，即125°45′。哥白尼从此数减去由岁差引起的6°45′，才能得出大约119°（对开纸170r第8行）。(120)哥白尼依据P—R（第十卷命题1帖号1v2），把这次观测误定在哈德里安4年（对开纸170r第18行）。 PS 1515也把年份定错了，认为是在哈德里安2年（对开纸109r）。PS(X，1)把年份定为哈德里安12年。按埃及的历法，哈德里安1年开始于116年7月25日，此时公认哈德里安开始和原来在位特拉强分掌最高权柄。因此哈德里安4年开始于119年7月25日。幸好哥白尼既没有用哈德里安4年，也未以119年作为进一步计算的基础。梅斯特林的N抄本（对开纸160v第16和18行）把哈德里安4年改为12年，并把119年改为127年。
(121)托勒密取太阳的平位置在天秤宫内17°52′，即为197°52′处。哥白尼从此数减去由岁差引起的6°39′，才能得出191°13′（对开纸170r倒数第13行）。
(122)托勒密取太阳的平位置在摩羯宫内21/15°，即为 272°4′处。哥白尼从此数减去由岁差差引起的7°4′，才能得出265°（对开纸170r倒数第8行）。
(123)托勒密取太阳的平位置在金牛宫内251/15°，即为55°24′处。哥白尼从此数减去由岁差引起的6°34′，才能得出48°50′（对开纸170v第5行）。
(124)相应于罗马历书中的正确日期为11月18日。哥白尼确实已开始写这个数字（对开纸170v第9行：xiiijCal）。但他没有继续写上正确的月份（12月），而改为1月，并把日期从14改成5。这也许是由于和托勒密于哈德里安21年对金星所作的另一次观测（PSX，1，最末一次观测）混为一谈了。梅斯特林在其N抄本中（对开纸161r第2行）把日期改为11月18日=罗马历12月14朔日，而A首次作公开的改正。
(125)托勒密取太阳的平位置在天蝎宫内25°30′，即为235°30′。哥白尼由此数减去由岁差引起的6°36′，才得到228°54′（对开纸170v第10行）。
(126)按弦长表，对44°50′为70，505，对44°40′为70，298，因此对44°48′为70，463.6，或在取半径=10，000时为7046。
(127)哥白尼在此处（171r第2行）取Ⅴ，20中托勒密第三次观测时的大距=471/3°。这也是他在Ⅴ，20中（对开纸170v第12行）原来所用数值。但后来他把该处的“1/3”划掉，并在右边缘代之以16′。然而此处在Ⅴ，21中他未作相应变化，而让“1/3”保留下来。可是在求DF的长度时他并非用47°20′，而用47°16′进行运算。按弦长表，对47°20′为73，531而对47°10′为73，333，因此对47°16′为73，451.8。在取半径=10，000时，哥白尼把后一数值写成7346。在另一方面，在取DBF=47°20′时，DF=7353。第谷在其B抄本中把对DBF应与47°相加的分数由1/3改为1/4（=15′，对开纸161r倒数第5行）。
(128)DF∶BD=7346∶10，000=7046∶9591.6。哥白尼把后一数值误写为9582（对开纸171r第5行），而由此数会得出DF=7353。
(129)AC∶DE=9791∶7046=1p∶431/6′；AC∶CD=9791∶209=1p∶
(130)AC∶DE=1p∶431/6′=10，000∶71941/3。哥白尼最终把后一数值写为7193，但原来此数后面有某一分数，被他擦去了（对开纸171r第9行）。AC∶CD=1p∶11/4′=10，000∶2081/3，哥白尼把后一数值写成“约为208”。
(131)托勒密取平太阳在宝瓶宫内251/2°，即为325°30′。哥白尼从此数减去由岁差引起的6°40′，才能得出318°50′（对开纸171r本章第 7行）。
(132)托勒密取金星位于摩羯宫内11°55′，即为281°55′。哥白尼从此数减去由岁差引起的 6°40′，才能得出275°15′（对开纸171r本章第 8行）。
(133)哥白尼由于笔误（对开纸171r倒数第7行）把sextante=1/6写为dex-tante=5/6。梅斯特林的N抄本（对开纸161v第22章第15行）改正了这个错误，而A（第385页）首先作公开的改正。
(134)哥白尼由于笔误（对开纸171r第1行）写上EGD。梅斯特林的N抄本和第谷的B抄本（对开纸161v倒数第10行）改为EGC，而T（第368页第6行）首次公开改正。
(135)按弦长表，对2°30′为 4362，对 2°20′为4071，因此对2°23′为4158.3，或在取半径=10，000时为416。
(136)哥白尼由于笔误（对开纸172r第8行）写为第20，但PS 1515所说“第29”（对开纸110v）是正确的。
(137)哥白尼在写33/4h=9dm32ds时（对开纸172r倒数第13行）出现笔误，把xxiij写成xxxij。3h45m=9dm221/2ds，他对尾数取略数为23。
(138)托勒密取太阳在人马宫内22°9′，即在262°9′处。哥白尼从数减去由岁差引起的6°39′，才能得出255°30′（对开纸172r，在被删去一段中的第 17行）。
(139)取月亮在 209°55′
和恒星在 209 40，
──
它们之间的距离为15′，可划分为11/2∶1=9∶6，
于是金星的位置为209°46′=209°5′-9′=209°40′
+6′。
对纬度按同样做法，
取月亮在 4°42′
和恒星在 1 20
──
(140)哥白尼由于笔误把BCE写成BDE（对开纸172v倒数第15行）。他在对开纸172v最末一行取CDF等于54°20′=2×27°10′，而在对开纸172v倒数第7行他取DCE(=BCE)=27°10′，因此CDF=2×BCE。在另一方面，很快可得BDE=28°[见下面注释(142)]。
(141)哥白尼画此图（对开纸172v）所取尺度和位置使他没有地方完全绘出金星轨道，并表出其与EF的交点L和与FK的交点K。读者从此图容易看出金星的远地点距离与近地点距离相差悬殊。由此得出的结果是金星的目视亮度应当有很大变化。但事实并不如此。因为哥白尼不能解释为什么没有这种变化，他采用对这类事情常用的办法，即保持审慎的缄默。他从未“指出托勒密无法说明金星亮度变化的错误”，尽管普莱斯对他进行毫无根据的攻击（见对“前言”的注释）。伟大的哥白尼主义者伽利略对这种情况更为了解。伽利略在其于1632年撰写的《对话集》(Dialogue)中指出，在第三天的对话中“哥白尼对金星大小的微小变化避而不谈…我认为这是因为他对于与这个学说如此不相容的现象无法得出使自己满意的解释”（《全集》，国家版，Ⅶ，362：12—15）。伽利略在这方面犯了一个不幸的错误，即认为金星自行发光或透明的想法来自哥白尼，而实际上哥白尼把这个概念归诸别人。N中的一处印刷错误造成伽利略的误解，而他的崇高威望使许多后来的作家都采用他的说法。参阅罗申(Rosen)“哥白尼论行星的位相和光度”(Copernicus on the Phasesand the Light of the Planets)，Organon，1965，2∶69—74．
(142)于是BDE=DCE+CED=27°10′+50′=28°。因为BDE=28°和CDF=54°20′，所以CDF≠2×BDE。此为上面注释(140)所改正的笔误。
(143)整个FDE=FDB+BDE=125°40′+28°=153°40′≠152°50′。哥白尼把BDE误取为BCE，因此得和=152°50′（对开纸173r第2行）。但是BDE=BCE+CED=27°10′+50′=28°。
(144)哥白尼的日期（xiij CalJanuarii，对开纸173r倒数第10行）=138年（原为139年）12月20日3 A．M．。这与他在对开纸172r第16—19行所取从基督纪元开始至托勒密观测的时间间距不符。该处所取间距为138y18d33/4h=
137个整年
138年1月至11月 334d
12月 15 33/4h
闰日（4—136年） 34
──
383
1 -365
── ────
138y 18d33/4h，或138年12月16日3A．M．
(145)哥白尼在此处（对开纸174v第17行）取这颗恒星的经度=1511/2°。这也是他的星表（对开纸60v倒数第5行）中的数值，在N中（对开纸54v）也是如此。后来哥白尼之外的某人把零弄模糊了，并在它上面写了一个不易识另的5。他为清楚起见在旁边的空栏内写上35。他得出151°35′。这大概是从托勒密所取室女宫内8°15′，即158°15′，减去哥白尼常用的岁差改正量6°40′，即得151°35′。
(146)哥白尼由于提前的重写错误，把正确的和数147°4′写成 144°4′（对开纸175r第1行）。
(147)弧KLG=半圆KL+(LG=
LFG)。哥白尼对180°加上EFG=72°
5′，而忘记从它减去EFL=CEF=1°21′。于是他得出错误值KLG=252°5′，而正确值为Me（第59页注释）所指出的250°44′。
(148)从基督纪元开端至1529年3月12日7∶30P．M．：
1528个整年
1529年1月至2月 59d
3月 11 191/2h
闰日（4—1528年） 382
──
452
1 -365
── ────
1529y 87d191/2h
哥白尼忘掉了从1529年3月12日午夜至正午的12h，因此他对1529y87d只加上71/2h（对开纸173v第6行）。梅斯特林的N抄本（对开纸163r第16—17行）把71/2h改为191/2，而A首次公开改正。
(149)哥白尼显然取托勒密·费拉德法斯13年12月18日破晓等于公元前272年10月12日3∶30A．M．：
272年10月 19d 201/2h
11月至12月61
271个整年
闰日 68
─── ─── ──
271y 148d 201/2h
+1529 87 191/2
──
──── 1 (24-)16h(=40dm)
1800y ────
236d
从基督纪元开端至哥白尼的观测历时1529y87d191/2h，见前注。
(150)从138年12月16日[并非20日，见注释(144)3∶45A．M．至1529年3月12日7∶30P．M．：
138年12月 15d 201/4h
1390个整年（139—1528年）
1529年 1月至2月 59
3月 11 191/2
闰日（140—1528年） 348 ──
1(24+) 153/4h
──
434
1 -365
── ────
1391y 69d 153/4h=39dm221/2ds，
哥白尼把尾数写为23ds（对开纸174r第5行）。哥白尼对此时段的计算表明他实际上是从12月16日算起。因此他想写xvij Cal．，而对开纸173r第10行的xiij Cal．只是一个笔误。
(151)哥白尼在此（对开纸174v第3行）写 91/2dm@33/4h，而在对开纸172r第19行所写为91/2dm=3h48m。
(152)哥白尼在此显然把第一届奥运会的开始时间定为公元前775年7月1日正午：
775年 184d
502个整年（774—273年）
272年1月至9月 273
10月 11 16h
闰日（772—276年） 125
──
593
1 -365
── ────
503y 238d16h=40dm
托勒密·费拉德法斯13年12月18日=公元272年10月12日，见注释(149)。
(153)虽然托勒密采用载轮模型，他并未使用任何这样的术语。然而阿拉伯作家提出了一个名称，它在译为拉丁文之后逐步演变成为“载轮”。这个名字见于阿耳·法尔加尼(AL-Farghani)著作的拉丁文译本[为十二世纪塞维尔的约翰(John of Seville)所译]，但在托勒密的《天文学大成》的拉丁文译本[为史列蒙纳的杰拉尔德(Gerard of Cremona)所译]中找不到这个词。后书于1175年译出，1515年出版，而哥白尼读到了它。他在P—R中（例如第九卷命题7）遇到过“载轮”一词。此书在1463年4月28日之前写成，但直至1496年8月31日才印出。
(154)根据普罗克拉斯的《评论》(Commentary)[莫罗(Morrow)译本第86页]，一条直线可由“多重运动[的积累]产生”。哥白尼把引用的普罗克拉斯的这句话写在对开纸176r的右边缘。列蒂加斯于1539春季把普氏《评论》希腊文本第一版以及欧几里得著作希腊文本第一版，作为礼物赠给哥白尼。因此哥白尼不可能在1539年之前写这个边注。假如他是从布鲁泽沃的阿耳伯特(Albert of Brudzewo)所著《皮尔巴赫论》(Commentary on Peurbach)（米兰1495年版）了解到这种产生直线的方法，他为什么要等到1539年并引用普罗克拉斯著作呢？哥白尼没有援引阿耳伯特的作品，这可能表明他不熟悉布鲁泽沃的《皮尔巴赫论》。
在另一方面，哥白尼在Ⅲ，4中一段删去的话里提到椭圆，这令人间接想起普罗克拉斯的这一段话。这位欧几里得评论家在此讨论一条直线，其两端在一个直角的两边上。举例来说，一个梯子的一端靠在垂直的墙上，而其另一端放在水平地面上。现在让梯子滑动，其上端沿墙壁往下滑，而下端离开墙壁运动。如果此时梯子的中点走出一段圆弧，则梯子上各点（两端除外）均在椭圆上运动。
有人把普罗克拉斯的图形误认为是图西的（《天文学史杂志》，1973，4∶129）。普氏的希腊文原意在该处翻译成下面一句话时受到歪曲：“如果我们设想一条直线靠在一个直角的两边上，则直线中心描出一个圆周”。但若直线靠在任何地方，它的中心就什么也描不出来。至于说直线的“两端作直线运动”，这也是误译。实际上希腊文原本说的是作“均匀”运动，而校订本说成为作“非均匀”运动。此外译文说“线心作曲线运动”，这也是误译。希腊文原本所说为“非均匀”运动。
进一步说，书中告诉我们“普罗克拉斯的目的是要论证怎样从两个直线运动得出一个圆周运动”。实际上，普氏思考的是简单线与复合线之间的区别。虽然圆周是一条简单线，但在给定条件下它可以由一种非均匀运动产生。
(155)哥白尼由于笔误把这个直径误称为HK（对开纸176v左边缘注释3第4行）。他在此处引用的图出现在对开纸176r上。T（第378页第13行）改正了他的错误。
(156)在哥白尼实际上称之为“水星逐日视差行度”的表中，与58d相应的值=3×60°=180°，因此对一整圈360°为2×58d=116d。
(157)157个整年
闰日（4—136年） 34d
138年1月至5月 151
6月 3 421/2dm=17h
188d
因此哥白尼把托勒密观测的时间定为138年6月4日克拉科夫时间5P． M．。
(158)托勒密取平太阳在双子宫内101/2°，即为
70°30′，哥白尼从此数减去
6 40便得
──
63°50′此为他所得的太阳平位置。
(159)140个整年
闰日（4—136年） 34d
141年1月 31
2月 2 12dm=4h48m
──
67d
因此哥白尼把托勒密观测的时间定为141年 2月 3日 4∶ 48A．M．。(160)托勒密取平太阳为在宝瓶宫内10°，即310°。哥白尼由此数减去由岁差引起的6°41′，以便求得平太阳的位置为303°19′。(161)哥白尼不用276°49′=第二次观测时的水星位置，而取第一次观测时的太阳位置=63°50′（对开纸177r第8行）。然而他在下面的计算中用的是正确值276°49′。
(162)托勒密取平太阳在天秤宫内9°15′，即为189°15′。哥白尼从此数减去由岁差引起的6°37′，便可求得他自己的平太阳位置182°38′（对开纸177r第14行）。
(163)托勒密取水星在室女宫内20°12′，即为170°12′。哥白尼从此数减去由岁差引起的6°37′，于是他应得他自己的水星位置为163°35′。然而他由于移项笔误把度数clxiij写成cxliij（对开纸177r第16行）。梅斯特林的N抄本（对开纸166r第8行）改正了这个错误，而A（第396页）首次公开改正。
(164)哥白尼在取“哈德里安的同一年”，即哈德里安19年，与基督纪元某一年相等时，并不认为这两个年份的时段相同。托勒密进行第一次观测是在埃及历3月，而第二次在埃及历10月。因为哈德里安的帝王即位纪年从夏季开始，托勒密的第一次观测是在公元134年，而第二次在135年。哥白尼把后一数字误写为Mcccv（=1305，对开线177r第18行）。如果他在本段最初注释中使用罗马数字cxxxv=135，则他在对开纸177r第18行就不会改用Mcc-cv。在另一方面，可以设想对开纸177r第18行把最初注释中的印度一阿拉伯数字135错误地改为Mcccv。如果这个情况能够代表哥白尼的经常作法，则可认为他实际上是用印度一阿拉伯数字私自进行运算，但后来为了出版的目的而把它们转化为传统的罗马数字。
(165)托勒密取水星位于金牛宫内4°20′，即等于34°20′。哥白尼从此数减去与岁差有关的6°37′，以便得出自己对水星所取位置27°43′（对开纸177r第20行）。
(166)托勒密取平太阳位于白羊宫内11°5′处。哥白尼考虑到岁差，从此数减去6°37′，以便得出自己对平太阳所取位置 4°28′（对开纸177r第21行）。
(167)按弦长表，对19°10′为32，832，对19°0′为32，557，因此对19°3′为32，639.5。哥白尼把后一数字写为32639（在对开纸177v第7行原为32649）。
(168)按弦长表，在取DBF=23°15′时，对23°20′为39，608，而对23°10′为39，341，因此对23°15′为39，474.5。哥白尼把后一数字写为39474（对开纸177v第8行）。
(169)哥白尼把线段AD误称为“ADC”（对开纸177v第10行）。他在上面不远处即第6行中出了同样差错，但他把该处的C删掉，从而改正了这个错误。然而此处的错误符号未予更正。
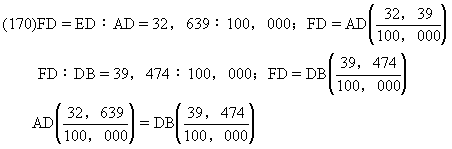
AD∶OB=39，474∶32，639=100，000∶82，684.8，哥白尼把后一数字写为82，685（对开纸177v左边缘，以此取代第10行中的一个错误值）。
(171)AC∶DE=91，342∶32，639=60′∶21′26″
AC∶CD=91，342∶8658=60′∶5′41″
(172)AC∶DF=91，342∶32，639=100，000∶35，732.9。哥白尼把后一数字写成35，733（对开纸177v第15行）。
AC∶CD=91，342∶8658=100，000∶9478.7。哥白尼把后一数字写为9479（对开纸177v左边缘）。
(173)129个整年
闰日（4—128年） 32d
130年 1月至 6月 181
7月 3 45dm=18h
──
216d
于是哥白尼取西翁观测的时间为 130年 7月 4日 6 P．M．。
(174)托勒密取平太阳位于巨蟹宫内10°5′，即为100°5′。哥白尼为改正岁差由此数减去6°35′，以便得出自己为平太阳所定位置93°30′。
(175)哥白尼由于笔误写成“之西”(praecedere，对开纸177v倒数第7行)。Z（第448页）改正了这个错误。
(176)分数应为2/3，而非3/4（dodrans，对开纸177v倒数第5行，Z第448页）。
(177)托勒密确定这次观测在12月24日。PS1515（对开纸106r倒数第15行）把日数误改为21。这无疑是哥白尼的错误的来源。
(178)138个整年
闰日（4—136年） 34d
139年1月至6月 181
7月 4 12dm=44/5h
──
219d
于是哥白尼把托勒密观测的时间误定为139年7月5日4∶48A．M．，而按前注正确日子应为7月8日。
(179)托勒密取平太阳位置为在巨蟹宫内10°20′处，即为100°20′。哥白尼为改正岁差从此数减去6°41′，以便求得自己为平太阳所定位置93°39′。
(180)托勒密取水星为在双子宫内20°5′处，这等于80°5′。哥白尼为改正岁差从此数减去6°41′，以便求得自己对水星所定位置73°24′。
(181)按弦长表，对3°0′为5234。哥白尼在取半径=10，000时把后一数字写为524（对开纸178r第17行）。
(182)因为哥白尼用 DF=422(+IF=212)作计算，他原来（对开纸178r右边缘）取CFI=634。他后来想到，为了求得CFI，他应把CF=524而不是DF与IF=212相加。于是他在删去634之后代之以737，后来又换为736加上1/2。他是在对开纸180r第3行已经写上737之后，把737改为7361/2。他在该处的第二个7上面重重地写一个6，并插进1/2。在此之前，他在对开纸178v在删掉一段之上的第5行也这样做过。
(183)参阅前面注释(168)。
(184)EF∶FH=10，000∶3947=10，014∶3952.53。哥白尼把后一数字写成3953（对开纸178r倒数第6行）。
(185)托勒密也有与哥白尼此处相当的论点，见PS，Ⅸ，8。
(186)EF∶FG=9540∶3858=10，000∶4044。哥白尼把后一数字写为4054（对开纸179r倒数第6行）。他得出这个结果是用FG=3868进行计算。在他于对开纸179r倒数第11行重重写上的5字下面，大概有一个被擦掉的6。这个数值(3868)应为3573（对开纸178v第4行）加上3/4×380之和。然而哥白尼把3/4×380误写为295。这大概是由于他在前面得到过1/4×380=95（对开纸179r倒数第14行），于是由于重写而出现差错。他在察觉这个错误后，把295改为285，并把3868改为3858。然后在查到4054时，把此数删去。但他不是代之以正确数值4044，而是在右边缘再次写上4054（不知是否为重写错误）。
哥白尼在取FG=4054时，取相应的角度=23°55′（对开纸179r倒数第5行）。按弦长表，
对24°0′为 40674
-23 50′ -40408
────────────
10 266
5 133
+23 50 +40408
────────────
23°55′ 40541
但他把分数从55减为521/2，他显然打算减少4054。可是我们在上面谈到，他没有实现这个意图。在取半径=10，000时，与角度23°521/2′相应的弦长应为 4047。
(187)哥白尼把经度和纬度上的长度弄巅倒了。他取经度距离为“2个月亮直径”而纬度距离为“1个月亮直径”（对开纸179v第11—12行）。可是托勒密把经度间距取成1个月亮直径而纬度间距为2个月亮直径。(188)按埃及人写分数的办法，除掉少数例外分子都为一。哥白尼一般不采用这种写法。然而他在此处所写的为“一半和三分之一”，这等于“六分之五”（对开纸179v第16—17行）。可是在他自己的星表中（对开纸61v第19行），和托勒密星表一样，这颗星的黄纬=1°40′，而非1°50′。于是我们在此处找到哥白尼提前重写错误的又一例。这是因为他在两行之下取1°50′为水星而非该恒星的黄纬。
(189)哥白尼由于对PS 1515中（对开纸108r第9行）一处内容的误解而说“在后来的4天中”（subsequentibus iiij diebus，对开纸179v倒数第11行），而托勒密的意思为“在此之后的第4天”。
(190)哥白尼原来（对开纸180r第3行）写的是737。后来他在第二个7上面重重地写上一个6，并插入1/2。这与他在对开纸178v右边缘和对开纸178r倒数第13行所作的修改是一致的。把CI的长度从737减少为7361/2，则与此相应地IF从212（对开纸178r倒数第13行和对开纸179r第4行）减成2111/2（对开纸180r第12行）。
(191)哥白尼在手稿中没有画这幅图。他取直径LM=380p，此为水星与其轨道中心距离的最大变化值[Ⅴ，27]。
(192)有人把这段话的意思误解为哥白尼从未看见过水星。勒威耶说过，哥白尼“从来不可能准备观看水星”[《巴黎天文台年刊》(Annales de l’Observatoirede Paris)，Ⅴ，1859，1—2]。德朗布尔认为“维斯杜拉河的薄雾使哥白尼从来不可能看到水星”[《现代天文学史》(Histoire de l’astronomiemoderne)，I，134]。大概是这句错误的论断引起勒威耶的误解。
(193)在瓦耳脱于1504年逝世五年之后，他的后嗣把他在纽伦堡的住宅卖给著名画家丢勒(Dürer)[《阿尔勃莱希特·丢勒的住宅及其历史》(Albrecht Dürer’s Wohnhaus und seine Geschichte)，纽伦堡，1896年，第4—6页]。瓦耳脱手书的观测记录归熊奈尔所有，熊氏于四十年后收这些记录在纽伦堡付印。这是在哥白尼逝世及其《天体运行论》在同一城市出版一年之后。瓦耳脱的教师列季蒙坦纳斯的一些著作和观测资料由熊奈尔编辑成册[《瑞几蒙塔纳斯的光辉数学著作》(Scripta clarissimi mathematici M.Joannis Regiomontani)，纽伦堡，1544年]时，把瓦耳脱的观测记录收为附录。威勒布罗德·斯涅耳(Willebrord Snel)在编辑黑斯(Hesse)的兰德格雷弗(Landgrave)的观测资料[《黑斯的天象和星体的错乱观测》(Coeli et siderum in eo errantium observationes Hassiacae)，莱顿，1618年]时，使瓦耳脱的观测记录第二次付印。第三次是成为Historia coelestis[奥格斯堡(Augsburg)，1666年]书中的一部份。该书编者化名为巴列塔斯(Barettus)，而非唐纳德·贝弗尔(Donald de B.Beaver)的“贝纳德·瓦耳脱”(Bernard Walther)中所称的“巴列西斯”(“Barethis”)（《天文学史杂志》，1970，1∶40）。
(194)瓦耳脱没有提到9月9日他进行观测所用仪器（Scripta...Re-giomontani，对开纸55r，页码误为59）。然而他在1491年8月26日首次观测水星时，他说他的仪器指向毕宿五(“Armillis rectificatis per Aldebaran”)；对8月31日的观测，他重复说“rectificatis Armillis ut prius”；而对9月2日的观测，他一次谈到“Armillis rectificatis iterum per Aldebaran”。在这方面应当提到，瓦耳脱毫不犹豫地使用毕宿五的阿拉伯名字Aldebaran。忠实于古代文化的哥白尼，把这个星名换为Palilicium。我们可以回想起，哥白尼在他的星表中列出金牛南眼的一等星时说，这颗星“被罗马人”称为‘Palilicium’”（对开纸58v末行）。
(195)瓦耳脱说“我发现水星是在室女宫内13°23′处”。哥白尼最初取分数为“大约五分之二”@24′，随后把这划掉并代之以“一个宫的1/4=15′（对开纸180v数第8—7行）。哥白尼在该页左边缘最后决定采用1/2°。对于哥白尼从23′到“大约24′”，再到15′和30′的接连变化，有些学者认为哥白尼有某种不良的或不诚实的动机。
(196)瓦耳脱在1491年对水星的观测，于8月26日开始，9月11日结束。在哥白尼所挑选的即9月9日的观测中，瓦耳脱谈到“水星看起来非常暗”。两天后瓦耳脱报告说：“9月11日，水星仍然可见，但很暗弱”。
(197)从基督纪元开始至1491年9月9日5 A．M．共历时1491y58d5h=1/2dm。
(198)哥白尼对149°48′=太阳的平位置加上由岁差引起的26°
59′，以便得出太阳的黄经176°47′。他在Ⅴ，23中取1529年的岁差=27°24′。
(199)约翰·熊奈尔(1477—1547)是一位受到正式任命的罗马天主教神甫。他任职直到造反的农民扬言要把所有神职人员处死为止。在此之后他在纽伦堡的一所高等学校教数学。正是他在1544年编印了瑞几蒙塔纳斯和瓦耳脱的著作。
(200)哥白尼所根据的资料(Scripta…Regiomontani，对开纸58r认为这次观测是“1月9日”进行的。哥白尼是一位人文主义者，他把这个日期说成是罗马历“1月13日之前5天”。这次观测是瓦耳脱做的，但哥白尼误认为是熊奈尔（对开纸18lr第3行）。哥白尼怎样会弄错了？
津勒尔(Zinner)说“哥白尼有熊奈尔向他报告的对水星位置三次测定的结果”[《约翰尼斯·米勒在由瑞几蒙塔纳斯命名的科尼西堡的生活和工作》](Leben und Wirken des Johannes Müller von Königsberg genannt Regiomontanus)，慕尼黑1938年版第173页，Osnabruck 1968年第二版第231页），似乎这是历史事实。但是没有丝毫历史证据表明，哥白尼和熊奈尔有过任何直接的联系。然而我们最近了解到，哥白尼“通过约翰·熊奈尔获悉…瓦耳脱对水星做过大量观测…也许哥白尼与瓦耳脱有过比较密切的关系，尽管这只是一种猜测。哥白尼在1496年底、1501年春和1503年春都可能路过纽伦堡，于是可能拜访过当时住在该城的瓦耳脱。看来哥白尼不会错过与瑞几蒙塔纳斯的这位著名学生见面的机会，但这两位天文学家是否聚会过却不得而知”[见注释(193)所引贝弗尔文第42页]。对哥白尼与瓦耳脱之间有过私人接触的证据，甚至还不如哥白尼与熊奈耳有过接触那样确切。Z不知怎样会弄错了并认为哥白尼在上一段开头处的说法“证明…他[哥白尼]通过熊奈尔收到瓦耳脱的观测资料”（第212页）。然而哥白尼的说法并不能证明这件事情，并且也没有对哥白尼取得水星的纽伦堡观测资料的过程提供任何资料。
由于误解此处Primum一词（对开纸180v倒数第12行）的含义，Z对哥白尼的错误说法提出一种不正确的解释。哥白尼所用的primum仅指瓦耳脱对水星所做三次观测中的“第一”次，而Z把Primum误译为“首先”(zuerst)。这意味着后者的观测是瓦耳脱以外的某人做的。照Z的说法，哥白尼“本已知道瓦耳脱死于1504年，因此并未进行全部[三次]观测”。但是瓦耳脱去世是在1504年6月19日，而1504年的两次观测是该年1月9日和3月18日做的。因此，如果哥白尼知道瓦耳脱逝世的日期，他就没有理由否定1504年的两次观测是瓦耳脱进行的。
那么，哥白尼怎么会出这个差错？并且他怎样取得瓦耳脱的观测资料？在列蒂加斯来到佛罗蒙波克与哥白尼会聚之前，他在纽伦堡拜访了熊奈尔。很可能是熊奈尔向列蒂加斯建议，他应当直接跟哥白尼学习新天文学。难道这不足以说明，列蒂加斯于1539年5月14日在去目的地的中途，在波兹南给熊奈尔的一封（已遗失）的信件中告诉他已经完成这次旅行（3CT第109页）？哥白尼在Ⅴ，35中引用了一个不寻常的词。他是从列蒂加斯于1539年带给他的一本书才知道这个词的。难道此处在Ⅴ，30中哥白尼使用列蒂加斯从熊奈尔处带给他的纽伦堡观测资料，就完全不可能吗？难道可以用瓦耳脱观测资料的编者熊奈尔的名字的出现来解释哥白尼的错误说法吗？在梅斯特林的N抄本中（对开纸169v第10行左边缘）有另外某人对此作了改正。
(201)哥白尼在对开纸181r第6行误写为“宝瓶宫”，而按书中内容显然应为“摩羯宫”。他在第6—7行取水星的位置为在太阳以西23°42′，而该行星为在摩羯宫内3°多（第3—4行）。于是位于27°7′的太阳应在摩羯宫内，而非在宝瓶宫内。哥白尼显然想到想在纽伦堡对水星所做的另一次观测。水星在摩羯宫内的位置为3°加一个分数。
哥白尼把此分数从1/4（第4行）改为1/3（右边缘）。因此，取太阳为在摩羯宫内（而非宝瓶宫内）27°7′而水星在同一宫内3°20′，则行星的西距角为23°47′。然而哥白尼把分数误写为42（xlij,第7行）。然而从他在后面Ⅴ，30的叙述（对开纸195r第5—7行）可知，他对这个间距所取数值实际上是23°47′。他在该处说，算出的距离23°46′与测出的距角“只差一点点”(Parum demunt)，因此实测值应为 23°47′。在梅斯特林的 N抄本中（对开纸169v第13—14行），其他某人把上述数值改为23°47′并把宝瓶宫换成摩羯宫。第谷的B抄本把宝瓶宫划掉，并在它上面写了摩羯宫的符号。
(202)哥白尼所根据的资料说的是“3月18日（Scripta…Regiomontani，对开纸60r）。哥白尼在此处又一次使用与之相当的罗马历日期，即”4月份朔日之前的15日（对开纸181r第8行）。
(203)哥白尼所根据的资料取水星为在白羊宫内26°30′处。他起先大概是由于疏忽把分数遗漏了，后来在右边缘插进了“cum deunce unius gradus”（当近于1度时）（取11/12°=55′，对开纸18lr）。但是N（对开纸169v第16行）把de-unce（十一分之一）误为decima（十分之一）（1/10°=6′）。梅斯特林认为decima是正确的。然而他想到这里有不当之处，于是在他的N抄本对开纸169v上写道：我想我们应取“位于27°缺1 10°”[=26°54′]。第谷也意识到有一个差错，于是在他的B抄本边缘写上“26°48′”。
(204)从1491年9月9日5 A．M．至1504年1月9日6∶30A．M．：
1491年9月 21d19h
10月至 12月 92
12个整年（1492—1503年）
1504年1月 8 6 30m
──
闰日（1492—1500年） 3
1(24+)h130m=3dm45ds
── ──
12y 125d
(205)按Ⅲ， 14末尾的逐年和逐日太阳简单均匀行度表，
对12y为 5×60° =300°
120d=2×60d 60
58 16 22
5d 4 55 40 56
3dm45ds@ 4
──────
-360
──────
哥白尼把后一数字写成120°14′（对开纸181r第16行）。
(206)按Ⅴ，1末尾的逐年和逐日水星视差行度表，
对12y 为4×60°=240°
120d=2×60d 6×60°=360
12 48 27
5d 15 32 18
3dm45ds@ 12
──────
-360
──
316°，
哥白尼在改正一项错误后把计算结果写为316°1′（对开纸181r第17行）。
(207)从 1504年 1月 9日 6∶30A．M．至1504年3月 18日7∶30 P．M．：
1504年1月22d 17h30m
2月 29
3月17 19 30
1(24+) 13h=321/2dm
──
69d
哥白尼把321/2dm写成31dm45ds（=12h42m，对开纸181r第18行）。
(208)按Ⅲ，14后面的逐日太阳均匀行度表，
对60d 为59°8′
9d 8 52
31dm45hs@ 32
──
68°32′=太阳的平均行度。哥白尼应把“行度”写为motus，而非locus（=位置，对开纸181r第18行）。
(209)哥白尼写的是281/2(xxviij s)，对开纸181r倒数第 7行）。
(210)取水星的远地点在 211°30′而第一次观测时太阳的平位置为149°48′，则太阳与该行星远地点的距离
=360°-211°30′=148°30′
+149 48
────
298°18′，哥白尼把此数写为298°15′（对开纸181r倒数第3行）。
(211)在第二次观测时，平太阳在 297°7′，在改正 27°8′的岁差后为
269°59′
-211 30
────
58°29′
(212)在第三次观测时，平太阳在5°39′，在改正27°8′的岁差后为
365°39′
-27 8
─────
338°31′
-211 30
─────
127°1′
(213)哥白尼起先用来表示这个角度的是另一些字母，后来把它们擦掉（对开纸181v第3行）并且（不正确地）代之以IEC。T（第389页第19行及注释）改正了这个错误。
(214)哥白尼（对开纸181v第17行）把此角误认作POM。Me（第62页注释）改正了这个错误。
(215)为了得出比值190∶105，哥白尼应当是用5519=sin33°30′=≮OPS进行计算。但他写的并非5519而是8349（对开纸181v倒数第15行）。他在此处显然打算取8339=sin56°30′=≮POS。他不仅把角度取错了，还把它的正弦值也抄错了。他大概是在零碎纸张上作计算，并在把（偶尔有错的）计算结果抄入手稿后就把这些纸张丢掉。
(216)哥白尼（对开纸182r第14行）把此角误称为CIF。T（第390页第30行）悄悄改正了这个错误。
(217)在手稿（对开纸182r）和N（对开纸170v）中都找不到这个小图。它是梅斯特林在其N抄本中补画的。与梅斯特林无关，T（第391页）也补充了这个图，但画蛇添脚地加上直径NR。Me（第320页）也仿照T这样做。哥白尼可能是无意中遗漏了这个小图，因为他正是在此处中断了V，30的写作。当此章由N的出版商排印时，责任编辑为奥西安德尔。假如列蒂加斯当时在纽伦堡，他由于对本书内容更为熟悉，会不会察觉并弥补这个遗漏呢？
(218)10000∶4535=190∶86。哥白尼把后一数字写成85（对开纸182r倒数第7行）。可是他在下面一行把此数与190相加，得和数却为276。
(219)哥白尼（对开纸195r第12行）把此角误称为CIE。T（第392页第4行）悄悄改正了这个错误。
(220)哥白尼由于重写错误（对开纸195r倒数第15行）把第二个角误为IEC。 W（第426页）改正了这个错误。
(221)从亚历山大之死至基督纪元开始，哥白尼（Ⅳ,7）算出共历时
323y130d12h
他在Ⅴ，29中定出这次古代观测是在 59 17 18h(=45dm)
────────
即在亚历山大死后 264y112d18h
对水星的第三次近代观测于1504年3月18日7∶30P．M．进行。
1503个整年
1504年1月至2月 59d
3月 17 19h30m
闰日（4—1504年） 376
──
452
1 -365
── ──────
1504y 87d 19h30m
+264 112 18
──────
1(24+) 13h30m=333/4dm
── ──
1768y 200d
哥白尼把日子的零数写为33dm（对开纸195v倒数第16行）。
(222)哥白尼在Ⅴ，1中取水星的年行度为3个整周再加大约54°。后一数值对开Ⅴ，1末尾附表中略有差异的数值也是适合的。现在有20×54°=1080°=
3个整周
+(20×3)=60
─
63
(223)哥白尼在此处（对开纸195v倒数第10行）漏掉表示“年”的字，
数字是由于预行重写而写错，因为VDLxx为下一行中的周数。梅斯特林在其N抄本中（对开纸172r第3行）改正了这个差错，而T（第393页第23行及注释）首次作公开更正。
(224)哥白尼在此处（对开纸195v倒数第11行漏掉“200”）。T（第393页第22行及注释）改正了这个差错。
(225)相应的现代数值为每63年大约6′21/3″（《天文学杂志》，1974，79∶58）。勒威耶首先指出，水星近日点行度的理论值与观测值不一致。西蒙·纽康姆(Simon Newcomb)证实这个差异的存在，并求得其数值为每世纪43″。这个偏差成为相对论的基础，被称为水星近日点的进动，比以前的理论所要求的每世纪多出43″。
(226)我们从上面的注释(221)可知，从基督纪元开始到1504年3月18日7∶30 P．M．共有1504y87d19h30m=483/4dm。哥白尼把后面的数字写成48dm。（对开纸196r第2行）。
(227)Ⅴ，1和该节末尾的水星逐日视差行度表都把水星的年日行度取为3°6′24″，从此值减去
59′8″，此为太阳的（即地球的）每日行度
────
2°7′16″，此为Ⅲ，14所取每日简单均为行度。
(228)哥白尼在此处（对开纸197v倒数第2行）使用希腊字“lemmation”。在他所查考过的拉丁文资料中找不到这个词，而他是从列蒂加斯于1539年送给他的《天文学大成》希腊文本第一版中读到它的。他在对开纸188r上开始撰写V，35，但只记下该章标题，然后用一个特殊符号注明此章不在其应有的位置上，而移到后面。这即是对开纸197v，是一张E型纸。他是在列蒂加斯到达佛罗蒙波克前几年才开始使用这种纸张（NCCW，Ⅰ，4）。因此1964年的俄文译本认为，哥白尼编写V，35不早于1539年夏季。GV（第十八卷第四章帖号ff8v）把阿波罗尼斯的定理称作inventum，而哥白尼原来用的词为demon-strata（V，3对开纸149v末行）。
因为哥白尼在1539年仍然忙于撰写第五卷后面几章，我们不难了解为什么列蒂加斯在该年9月23日写成的《第一报告》（First Report）中谈到，哥白尼“已经大部份完成了”他的工作（3CT第162页）。列蒂加斯在威吞堡的一位朋友于1541年4月15日告诉麦兰其松（Melanchthon）说，列蒂加斯“从普鲁士函告，他正在期待他的老师〔哥白尼〕完成其著作”。直至1541年6月2日，列蒂加斯仍然报告说，他的“老师…正在大量写作”。
(229)哥白尼原来写的是“扇形AEG”（对开纸198r第17行）。他后来想起“扇形AEG”居于第二个比率，而非第一个。于是他删掉“扇形”一词，但是忘记把扇形的符号从（AEG）改为三角形所要求的符号（AEC）。T（第405页第1行及注释）改正了这个错误。
(230)在第二个不等式中，哥白尼把直线GE误写为GF（对开纸199r第1行）。Mu（第369页第32行注释）改正了这个错误。
(231)N把CM印成CL（对开纸180v倒数第15行）。这不是一般的排印错误。N取第二次留在L，而非M；它画直线ELM，而非EMN；它把LM的一半而非MN与LE而非ME相比较；它取第二次留在L而非M点；此外它提到的是弧FCL，而非FCM。N所用的这些符号在手稿中确实出现（对开纸199r第9—13行）。然而手稿把N中的这些符号统统删掉，而代之以英译本的这些符号。这个情况该如何解释呢？无论如何在列蒂加斯为付印而抄录手稿时，还未作这些改动。因此可认为在列蒂加斯于1541年底离开佛罗蒙波克之后，哥白尼还继续修正他的手稿。N是根据列蒂加斯的抄本（我们可称之为半确定本）印出的。梅斯特林的N抄本（对开纸180v）改正了这些错误。
(232)哥白尼说“画…DG垂直于EFB”。但在对开纸199v上画出直线DG之后，他在它上面画五个叉号，表示应当删去。他这样做大概是因为他在早期版本中用的是三角形DFG，而在印刷版本中没有用它。他想到不需要使用直线DG，便把它删掉。但在这样做的时候，他忘掉以前所说的“画DG”。
(233)这个乘积63963984（对开纸200r倒数第5行）是哥白尼偶尔会犯的重写错误的又一例。第四和第五个数字应为51，而不是63的重复。(234)DE∶DA=10，000∶6580=60p∶39p28.8′。哥白尼把后一数字写为29′（对开纸200v第3行）。
(235)99p29′×20p31′=2041p3.9′。哥白尼把后面的数字写成4′（对开纸200v第5行）。
(236)2041p4′÷3p16′14″=7347840″÷11774″=624p4.4′。哥白尼把后一数字写为624p4′（对开纸200v第8行）。
(237)DE∶EF=60p∶24p58′52″=216000″∶89932″=10000p∶4163p31′。哥白尼把后面的数目写作5′（对开纸200v左边缘）。
(238)DE∶DA=10，960∶6580=216，000″∶129，678″=60p∶36p1′18″50p。哥白尼把后面的数字写为20″（对开纸201r第13行）。
(239)AE×EC=96p1′20″×23p58′40″=345，680″×86，320=29，839，097，600″÷12，960，000=2302p23'56″。哥白尼把后面的数目写为58″（对开纸201r第15行）。
(240)DE∶DF=60p∶30p4′51″=216，000″∶108，291″=100，000∶50，134.7。哥白尼把后一数字写为50，135（对开纸201r倒数第15行）。
(241)DE∶AD=9040∶6580；60p=216，000″×6580=1，421，280，000″÷9040=157，221″=43p40′21″。
(242)DE∶EF=60p∶18p59′58″=216，000″∶68，398″=100，000∶31，665.7。哥白尼把后一数字写为31，665（对开纸201v第7行）。
(243)手稿第五卷处于紊乱状态，以致哥白尼没有标明它在何处结束。N标明此处为本卷之末，以后各版均仿此。