感觉的分析
作者: 恩斯特·马赫
第十章 各个视觉相互之间以及它们与其他心理要素之间的关系
各个视觉在正常的心理生活中并不是孤立地出现的,而是与其他感官的感觉结合在一起出现的。我们看不到视觉空间中的视象,而是知觉到我们周围具有各种各样的感性属性的物体。只有作有目的的分析,才能从这个复合体中分出视觉来。但知觉整个来说也几乎是与思想、愿望、欲求结合在一起出现的。感官的感觉会引起动物符合于生活条件的适应运动。如果这些生活条件是简单的,变化很小并且缓慢,则用感官就足以直接引起适应运动,而决不需要高度的智力发展。在各种复杂的、变化多端的生活条件下,情形则不然。一种很简单的适应机制不可能在这里发展,更不要说达到目标了。
低等动物吞食一切进入它附近的、引起适度刺激的东西。高度发达的动物则必定是冒着风险觅食的,在发现食物时,要机智地抓住它或狡猾地捉弄它,并且小心翼翼地检验它。在一种食物的回忆强烈到足以胜过对抗的考虑,并引起相应的运动以前,必定浮现出一整系列不同的回忆。因此,在这里与感官感觉相对峙的必定有一定量的共同决定适应运动的回忆(或经验)。在这当中就有智力。
在处于复杂生活条件下的幼小高等动物中,引起适应运动的感官感觉的复合体往往带有很复杂的性质。幼小哺乳动物的吮乳与幼小麻雀的行为(已在第61、62页描述过)就是很好的例证。随着智力的发展,引起适应运动的这个复合体的部分总是变得越来越小,而感官感觉则越来越多地为智力所补充和代替,就象我们日常在儿童与成熟动物身上可以看到的那样。
在本书1886年版的一个注释中,我曾经警告说,要谨防当时还流行的那种过高估计低等动物智力的倾向。我的看法的依据不过是对甲虫的机械运动、蛾子的向光飞行等等所做的偶然观察。后来出版了勒卜的一些重要著作,它们给这个看法提供了坚实的实验基础。
现在,低等动物心理学又成了一个争论甚多的领域。当贝特(A.Bethe)依据对蚂蚁和蜜蜂所作的富有意义的有趣观察,主张一种极端的反射理论,认为这类动物是笛卡尔讲的机器时,细心的批判的观察者,诸如瓦斯曼(E.Wasmann)、布太尔-雷彭(H.v.Buttel-Reepen)和福雷尔(A.Forel),则认为这类动物有真正高级的心理发展过程。连高等动物心理学现在也又引起了普遍的兴趣。策尔的一些主要是写给广大公众的著作,包含着某些很好的观察与妙见,似乎以审慎的方式既没有高估也没有低估动物。
谁曾经研究过生理学,甚或仅仅赞赏过戈尔茨的著作,谁就会了解反射对于任何动物有机体、甚至最高人类有机体维持生命所具有的重要意义。谁要是进一步观察,那种记载个体经历的记忆对生物反应的影响怎样随着组织的简化而极其令人注目地减少,谁就会有一个自然而然的想法,即试验比较简单的有机体的行为是否和在何种限度内可用单纯的反射来理解。诚然,那些完全没有记忆而只靠绝对不变的反射的动物有机体是不可能存在的,因为在个体的获得性与物种的获得性之间几乎不可能划出一条严格的界限。然而,我以为做这样一种试验是很有贡献的,当然,批判地解释试验结果会更有价值。
我希望,我们不仅能从我们的儿童身上,而且也能从动物这个“我们的年轻兄弟”身上学到很多有关我们的心理学的东西。但要了解人为什么在心理方面胜过最聪明的动物,则应充分重视物种与个体在数千年社会文化气氛中获得的东西。参看附录14。
因此,表象必须代替不完全的感官感觉,并进一步编制最初唯独由感官感觉决定的过程。但在正常的生活中,表象却完全不能永远排挤现存的感官感觉,除非有机体遇到极大的危险。实际上,在正常的心理生活中这两种心理要素之间存在着很大的差别。我看面前的一块黑板。我能极其生动地在这块黑板上想象一个用清晰的白线画出的六角形或一个有色图形。但除了病理情况以外,我总是知道我看到的东西和我自己想象的东西。我感觉到,我在过渡到表象时,怎样转移眼睛的注意力,使它转到别的方向。这种注意力就象第四座标线一样,区分了在黑板上看到的斑点与在同一部位想象的斑点。如果我们说映象笼罩在所视的东西上,犹如映现到透明玻璃片中的镜象笼罩在由此看到的物体上一样,那么这并不会完全把事实描述清楚。反之,我觉得想象的东西是受一种质上不同的、对抗的感性刺激的排挤的,并且有时也反过来排挤这种感性刺激。这暂且还是一个心理学事实,它的生理学解释诚然也有待于发现。
自然应该假定,在表象活动中甚至同样一些有机过程又会部分地通过中枢神经系统器官的相互作用而重新活跃起来,而这些器官在相应的感觉活动中是由物理刺激决定的。表象在正常情况下不同于感觉,乃是由于表象的强度微乎其微,但主要是由于它有不稳定性。如果我在表象中给自己画一个几何图形,情况就会这样:在线条画出以后不久,一俟我的注意力转向其他线条,似乎它们就消失了。在返过来看这些线条时,我们不会再看到它们,而必须重新再把它们创造出来。这种情况表现的主要是实际的几何作图相对于想象的几何作图所具有的优点与方便。少量的线段,例如,同一个圆弧上的圆心用与圆周角,它们带有一对重合的或相交的边,我们是易于在表象中保持的。但如果在这种情况下再通过圆周角的顶点添加直径,那么,如果不连续恢复与补充图形,就很难以在表象中推导出角度的比例关系。此外,反复更替图形的熟练程度和敏捷程度还会由于练习而得到异常的提高。当我研究斯坦纳尔(Steiner)与封·斯陶特(von Staudt)的几何学时,我所能做出的成绩要比我现在可能做出的更多。
智力的迅猛发展取决于人类的复杂的生活关系,表象会由于这种发展而顿时全然受到注意,以致有识之士周围的一些过程没有被看到,向他提出的问题没有被听到,这种情况被不习惯于做这件工作的人们称为“心不在焉”,但更恰当地说,可以称为“思想集中”。如果现在当事人在这样一种情况下受到干扰,那么,他会很清楚地感觉到替换注意力时所做的功。
注意表象与感官感觉之间的这种差别,很适合于防止感觉现象的心理学解释中的漫不经心。假如我们更多地注意到了这个情况,著名的“无意识推论”学说就决不会得到这样广泛的发展了。
以自己的状态决定表象的器官,我们可以暂时设想为这样一种器官,这种器官(在很小的程度上)能够提供感觉器官与运动器官的一切特殊能量,以致按照它注意的性质与方向,时而器官的这种能,时而器官的那种能就会对那决定表象的器官发生影响。这样一种器官特别宜于沟通不同的能之间的生理学联系。象对切除大脑的动物的经验告诉我们的,在这里除了“表象器官”以外,可能还有许多其他类似的、与大脑没有什么密切联系的联络器官,因而它们的过程并未进入意识。
如我们从自我观察了解到的,丰富的表象生活诚然是在人类身上才出现的。这种生活表现完全说明了有机体的一切部分的相互关系,它的一些开端也诚然存在于动物进化系列的低级阶段。但某个器官的各个部分也必定通过它们彼此的紧张关系,而有这样一种关系,这种关系同整个有机体各部分的关系是类似的。两个视网膜及其依赖于光感觉的适应运动装置与遮光运动装置,提供了关于这样一种关系的一个很清楚的与熟知的例证。生理学实验与简单自我观察告诉我们,这种器官有它自身的、合乎目的的生活习惯,有它特殊的记忆,并且我们几乎可以说,有它自身的智力。
与此有关的最有教益的观察是由约翰·缪勒在其佳作《论视觉幻象》(考勃林茨1826年)搜集到一起提出的。缪勒等人在清醒状态中考察过的视觉幻象完全不受意志与思考的影响。正是一些独立的、实质上受感官约束的现象,在自身完全带有所视客观东西的特性。这是感官中的真正的幻觉现象与记忆现象。缪勒以为,幻象的自由独立的生活是有机生命的一个部分,是同所谓联想律不相容的,他很怀疑联想律。我觉得,缪勒描写的幻觉的连续变化并不违背联想律。倒不如说,这些过程简直可以被理解为对于现象在脑海中呈现的缓慢变化的回忆。只不过由于时而这个感觉领域,时而那个感觉领域开始也起作用,才在通常的表象联想过程中出现了飞跃性的东西。(参看本书第11章)
在“视觉实体”(按照缪勒的说法)中通常作为视网膜兴奋的结果发生的、决定视觉活动的各个过程,也可以作为例外,在没有视网膜兴奋的情况下自发地出现于视觉实体,而成为幻象或幻觉的源泉。当幻象以其特性强烈地结合在以前所视的东西上时,我们所说的是感性记忆;当幻象比较自由地和未经中介地出现时,我们所说的就是幻觉。不过,这两种情况之间的严格界限几乎无法加以肯定。
我从亲自观察中熟习了一切类型的视觉幻象。幻象同看得不清楚的东西混合起来,又部分地排挤这种东西,这种现象出现得极其频繁。我在疲倦地于夜间乘火车旅行以后,就特别清楚地看到这些现象。那时一切岩石与树木都采取了极其离奇的形式。当我在几年前深入研究脉搏曲线和脉搏描记法时,黑色背景上的细致白色曲线常常在夜间与阴天极其清晰和实在地呈现在我眼前。甚至在后来我从物理学方面作不同的研究时,也看到“感觉记忆”的类似现象。我以前未曾看到的形象很稀奇地在白天呈现在我眼前。例如,几年以前有一种鲜红的毛细网络(类似乎所谓的神奇网络)连续地在好几个白天映现在我读的书或我写的纸上,而我当时并未研究这类形式。我在幼年时期往往在入睡以前看到着色鲜艳、变化多端的地毯模样;如果我把注意力转到这个方面,这种现象现在也会出现。我的一个儿童也常常告诉我说,他在入睡以前看到了花朵。很古怪的是我在夜间入睡以前看到各种各样不随我的意志而变化的人物形象。有一次偶然的机会,我在试验中成功地把一个人的面部看成了一个无肉有骨的头颅,但这种个别的情况也可能是偶然的。在暗室中苏醒时最后梦见的形象依然以其鲜艳夺目的颜色保存下来,这种现象经常在我这里发生。若干年来我经常遇到的一个独特现象是这样的:我睡醒后合上眼睛安静地卧在床上,我在自己面前看到了白天盖在床上的床罩和一切折叠起来的东西,在床罩上我的手完全静止不动,也没有什么变化;如果我睁开眼睛,则这时不是完全天黑,便是已经发亮,但床罩和我的双手却与我刚才看到的迥然不同。这是一种特别固定的与长久的幻象,它是我在其他情况下未曾观察到的。我以为,可以从这个映象看出,一切部分尽管相距甚远,也能用一种根据已知原因不可能在所现客体上看出来的方式,同时在一起清楚地表现出来。
在我青年时期,常常在睡醒以后很清楚地出现一些听觉幻象,尤其是触觉幻象;但自从我的音乐兴趣剧减以来,它们已经变得极罕见和十分贫乏了。不过,音乐兴趣也许是派生的、被决定的东西。
如果使视网膜不受外部刺激的影响,而把注意力唯独转向视野,则几乎总是有幻象的痕迹。诚然,在外部刺激软弱模糊时,在环境半明半暗时,或在我们观察带有微弱斑点的平面、云彩或灰墙时,这些痕迹就显示出来。我们后来想要看到的形状,就它们不是依赖于注意力对看清的斑点的单纯选择和综合而言,无论如何不是想象的幻象,而至少部分地是自发的幻象,它们有时必定在局部地方离开视网膜的刺激。在这些情况下我们的期待似乎有利于幻象的出现。在寻找干扰带时,我常常以为在视野中清楚地知觉到了幻象的最初微弱痕迹,但实验的不断进行则使我确信我确实发生了错觉。在半明半暗的空间里我以为自己反复明显地看到了我所期待的水从橡胶管里流了出来,但我在用手指去摸时却发现自己弄错了。这样的微弱幻象似乎对智力的影响颇有伸缩性,而智力则不能对强烈的、着色鲜艳的幻象产生任何效果。前者接近于表象,后者接近于感官感觉。
这些微弱的幻象时而被感官感觉压倒,时而与感官感觉保持平衡,时而排挤了感官感觉,这就提供了把幻象的强度与感官感觉的强度加以比较的可能性。斯克里普彻(Scrinpture)已经提出这个思想。他在一位自以为看到十字形线条(它实际上并不存在)的观察者的视野里,让一条真实的直线从预料不到的方向出现,其强度从零开始逐渐增长,以至这条直线被察觉出来,并被认为与幻象是等价的。这可以证实从感觉到表现的一切过渡。无论在什么地方,我们都得不到一种心理要素,它似乎完全可以同那种无疑须被视为物理对象的感觉加以比拟。各个表象的(联想的)关系当然不同于各个感觉的关系。
列奥纳多·达·芬奇(见第54页所引书)关于幻象与所视客体的混合说过如下的话:
“在这些指示下给一种新发现的观点以一席地位,我是不会忽略的;这种观点尽管显得是微不足道,几乎是滑稽可笑的,但对于激励心灵去作各种各样的发现却同样很有用途。这种观点的实质在于:你看某些满布各式斑点的墙壁或带有各种不同混合物的石头,如果你有某种发明的能力,你就会在那里看到一些类似于各种风景的东西,它们用各种山脉、河流、岩石、树木、大平原、小丘与峡谷装饰起来。你也会在那里看到各式各样的战役,看到奇特陌生的人物的清晰部位、面部表情、风俗习惯以及你可能认为形式完善的无数东西。在这类墙壁与混合物上出现了类似于钟响时出现的东西,在敲钟时你会又发现你想象的每个名称与每个词汇。
“可不要小看我的这个看法,我抱着这个看法劝你,有时停止不动,观看墙上斑点,或观看火中灰烬、空中云彩、地上泥土或其他这样的地方,这也许对你不会显得是一种累赘;如果你真正观察它们,你会从中得到很令人诧异的发现。因为画家的心灵会受到(它们的)激励,去作出(这样的)新发现,无论这是在对战役、动物和人作构图,还是在对风景和诸如魔鬼之类的可畏东西作构图,它们都已经令你心醉如迷。因为紊乱的和不确定的东西会唤醒心灵作出新的发现。但你可要首先注意,你要懂得很好地构造你想表现的东西的一切部分,例如生物的四肢以及风景的各个部分,即石块、树木和诸如此类的东西”。
在视网膜不兴奋的情况下很强烈地独立地出现幻象,除了梦境与半醒状态以外,这必定会因为生物学上不合乎目的而被视为病理学的。同样,我们也必定可以把幻象对意志的任何反常的依赖性称为病理学的。在那些认为自己力大无比,认为自己是上帝的精神病人身上,就可能出现这样的情况。但单纯缺乏抑制性联想,也同样能导致妄自尊大的狂想。例如,有人在梦境中会以为他已经解决了最大的问题,因为在这里没有发生揭示矛盾的联想。
在预先作了这些说明以后,我们想考察若干生理光学现象,它们虽然尚未得到充分的解释,但作为感官的独立生活的表现,相对说来还是最容易理解的。
我们通常都是用双眼看东西,对于为生活服务的特定目标来说,看到的不是颜色与形式,而是空间中的物体。在这里具有重要意义的不是复合体的各个要素,而是整个生理光学复合体。如果这个复合体由于特殊情况而表现得不完全,眼睛就试图按照在其生活条件中获得的(或遗传下来的)习惯去补充这个复合体。在用单眼看东西或用双眼看遥远的东西的时候,如果在眼睛距离方面体视差别消失了,则容易出现这类情况。
我们通常知觉到的不是光明与阴暗,而是空间中的对象。物体自身的阴影是几乎察觉不到的。光亮度的差别引起深度感的差别,并且有助于模拟物体,在这里已不再象观看遥远的山脉时很引人注目地看到的那样,单凭体视差别就足以达到模拟物体的目的。
从这方面来看,照相机的模糊底片上的映象是颇有启发意义的。在这里有人常常对光明的亮度与阴影的深度感到惊奇,只要他们无需在一个平面上看到每样东西,他们就完全不会在物体上察觉出这种亮度与深度。我很清楚地回想起在我的童年时代,图画上的任何浓淡不同的色彩我都觉得是不合理的和歪曲真相的,而一幅轮廓画则使我感到很满意。同样,大家都知道,有些民族,如中国人,整个来说虽然其艺术技巧是发达的,但是却完全不能画出浓淡参差的色彩,或只能以有缺陷的方式画出这样的色彩。
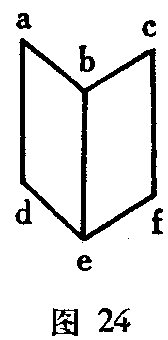
我在很多年以前做过的下列实验,很清楚地说明了光亮感与深度感的上述关系。我们把一张打折的名片放在我们面前的写字桌上,使它的折叠的边bc朝向我们。令光线从左侧射入。这时名片的一半abde更亮,另一半bcef则更暗,但这种情况在不抱先入之见的观察过程中几乎不可能觉察出来。我们在这时闭上一只眼睛,空间感觉部分就消失不见了。我们总是依然看到折叠的名片在空间中,而在照亮的地方刚看不到任何引人注目的东西。但一俟我们不看叠起的边be,而看一个凹入的边,光亮与阴影就会象涂上了覆盖颜色一样呈现出来。我暂且不考虑这种容易解释的名片透视倒置。这样一种“反演”是可能的,因为深度并不取决于单眼映象。假如在图25的1中o代表眼睛,abc代表打折名片的截面,箭头代表光线的方向,则ab显得比be更亮。同样,在2中ab也比bc更亮。如我们看到的,眼睛必定获得一种习惯,也把深度感的落差与所现平面要素的亮度相置换。如果光线从左侧射入(1),落差与深度则会随着亮度的减低而向右减低,如果光线从右侧射入,情况则相反。既然嵌着视网膜的眼球的外皮是透明的,所以,光从右侧射入还是从左侧射入,也就对光在视网膜上的分布不是无关紧要的事情。因此,这种情况完全是这样安排的,即不借助于任何判断的力量,眼睛也能形成一种固定的习惯,它以特定的方式使亮度与深度联系起来。如果象在上述实验里那样,能借助于另一种习惯,使一部分视网膜同前一种习惯相冲突,则这种结果会通过明显的感觉表现出来。
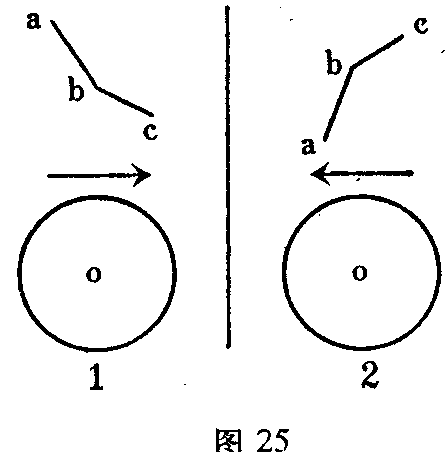
透过眼球外皮的光线的效果能有多么重要的意义,可以从费希纳的某些实验得知。属于这方面的一个观察是这样的:在我的写字桌下铺着一块灰绿地毯,而我在写字时只看到它的一小块。如果明亮的阳光或曙光从左侧射入,意外地或有意地产生了关于那一小块地毯的双象,那么,受到强烈照耀的左眼的映象就会通过对比,呈现鲜艳的绿色,而右眼的映象则完全是颜色模糊的。在这后一种情况下,在反演实验中,研究照射眼球的强度与颜色的变化也许是有趣的。
以上所述只能表明现象的特点,指出寻求生理学解释(心理学思辨除外)所遵循的方向。我们还想说明,在相互关联的感觉的性质方面,似乎有一种类似于能量守恒定律的原理在起支配作用。亮度的差别部分地转变为深度的差别,而且在这个过程中变得更弱了。另一方面,亮度的差别之所以能增大,是以牺牲深度的差别为代价的。一种类似的说明今后还会在另一场合作出。
观察物体的习惯,即注意属于光感觉的、在空间上关联的更大质块的习惯,引起了一些独特的、有时令人惊讶的现象。例如,具有两种颜色的油画或图画每每按照人们把这一种或另一种颜色理解为背景,而一般看起来迥然不同。大家都知道这个令人迷惑不解的图形,一俟人们把明朗的天空理解为对象,而把暗色的树木理解为背景,在树干之间就呈现出一个幻影。只有在例外的场合,背景与对象才表现出同一种形式,在这种形式中包含着一种经常使用的装饰动机,举例说,关于这种现象可以见之于取自上述《装饰文典。第15页的图26,也可以见之于取自那部著作的插图45的图20与图22,取自它的插图43的图13。

在单眼观察透视图时出现的空间视觉现象,或换一个结果相同的说法,在单眼观察对象时出现的空间视觉现象,通常很容易被当作几乎是自明的。但我认为,对于这种现象还应作各种研讨。可能属于无穷多不同对象的同一个透视图,仅仅部分地决定了空间感觉。因此,虽然在涉及这种图的许多可思议的物体中只有很少的物体实际上被看到,并且具有完全的客观性的特点,这种现象也必定具有有力的生理学根据。这可能不是基于对附带的属性的追忆,不是基于对浮现在我们脑海中的自觉回忆,而是基于视觉感官的特定生活习性。
如果视觉感官是按照它在物种与个体的生活环境中获得的习性活动的,那么我们便可以首先假定,它是按照概率原理进行活动的,也就是说,那些最频繁地被一起引起的功能只要其中有一种功能受到刺激,也就会一起出现。例如,那些最频繁地与某个透视图相关的深度感觉,如果这个图出现了,而这类感觉并未在此中共同起决定作用,也易于被再现出来。此外,似乎在看透视图时还表现出经济原理,也就是说,视觉感官本身承担的努力决不大于刺激决定的努力。如我们将会看到的,这两条原理的结果是一样的。
我们想详细地解释刚才作出的论述。如果我们观察透视图中的一条直线,我们会把这条直线总是看作空间中的一条直线,虽然作为透视图的直线可以对应于作为对象的无穷多不同的平面曲线。但是,只有在曲线平面穿过一只眼睛的中心这个特殊场合,曲线平面才在有关的视网膜上映现为直线(或最大的圆圈),并且只有在曲线平面穿过两只眼睛的中心这个更为特殊的情况里,曲线平面才对双眼映现为直线。因此,很可能一条平面曲线表现为直线,而空间中的直线则总是在两个视网膜上映现为直线。因此,对应于透视直线的最可能的对象就是空间中的直线。
直线有多种几何学特性。但是,例如直线是两点之间最短的线段这个尽人皆知的几何学特性,在生理学方面就没有重要意义。比较重要的是:在中央平面中存在的或对中央平面垂直的直线在生理学方面是自相对称的。此外,在中央平面存在的垂直线还以深度感觉的最大均匀性以及这种感觉与重力方向的重合为其生理学特征。一切垂直线都容易被迅速地弄得与中央平面重合,因而分享这种生理学的优越性。但空间中的直线一般必定还以其他某种东西为其生理学特征。直线的一切要素的方向都相同,这是早已指出的事实。但对应于空间中的直线的每个点的还有相邻各点的深度感觉的平均值。因此,空间中的直线表现出了对于深度感觉平均值偏离的最小限度,就象直线上的每个点表现出相邻各点的同类空间值的平均数一样。由此显然可以假定,直线看起来是用力最小的。所以,当视觉感官向我们显示为偏爱直线时,它所进行的活动既遵守经济原理,同时也遵守概率原理。
还在1866年我就在《维也纳科学院会刊》第54卷上写道,“既然直线总是到处围绕着文明人,所以我们可以假定,视网膜上任何可能的直线都无数次以任何可能的方式被看成空间中的直线。因此,眼睛解释直线图象的熟练程度就可能使我们不感到惊奇”。我当时写这段话(与我在同一篇论著中支持的达尔文主义观点相反),抱的决心不大。现在我比以前更加确信,上述能力决不是个人锻炼的结果,甚至完全不是人类锻炼的结果,而是动物也有这种能力,它至少部分地是遗传的东西。
一种感觉对相邻感觉的平均值的偏离一般总是令人注目的,并且引起感官的特别努力。曲线的任何弯度,表面的任何上凸与下凹,总是意味着一种空间感觉对引起注意的周围空间感觉的平均值的偏离。平面的生理学特征在于那种对平均值的偏离是最小限度的,或者专门就每个点来说,是等于零的。如果我们通过体视镜观察:一个有斑点的表面,其部分图象尚未统一为双眼图象,则在有斑点的表面突然伸展为无斑点的平面时,会造成一种特别令人舒适的印象。对圆圈与球体的美感印象似乎在本质上就是建立在这样的基础上的,即上述对平均值的偏离对所有的点来说都是相同的。
对周围环境感觉的平均值的偏离在光感觉方面也起作用,这是我在许多年前的一篇著作里指出来的。如果象图27所示,我们把一系列黑白相间的扇形画到一条纸带AABB上,然后把这条纸带卷到圆柱上,圆柱的轴平行于AB,则在圆柱迅速旋转时会出现一个亮度从B到A逐渐增大的灰色场,而在这个场中突现出更亮的纸带αα与更暗的纸带ββ。对应于凹处α的一些部位在物理学上不比周围的环境更亮:但它们的光亮强度超过了邻近的环境的强度平均值,而β处的强度则反而总是在环境的平均强度之下。因此,这种对平均值的偏离可以清楚地被感觉到,从而给视觉器官负担了一项特别的工作。反之,只要每个点的亮度相当于邻近各点的平均值,亮度的连续变化就几乎察觉不出来。这种情况对于对象的突出与定界具有什么目的论意义,我在很久以前(上引文,《维也纳科学院会刊》1865年10月与1868年1月)已经指出。视网膜抹煞了微小的差别,而不按比例地突出了较大的差别。视网膜变得机械和呆板了。潘诺慕在他那个时代就已经注意到了轮廓对视觉的意义。

通过很多实验(图27所示是其中最重要的一个实验),我获得了一个看法,认为一个视网膜部位的亮度是按照偏离开相邻部位亮度的平均值的大小感觉到的。因此,这个视网膜部位在那平均值中的份量可以设想为随着离开被观察部位的程度而迅速减少;当然,这只有通过视网膜要素的有机相互作用才能理解。假定i=f(x,y)是涉及一个座标系(x y)的视网膜照亮强度,则那个对任一部位都有决定意义的平均值是通过i+m/2(d2i/dx2+d2i/dy2)近似地(象征地)表示出来的,在这里表面f(x,y)的一切曲率半径都被认为相对于那段还有视网膜部位的显著影响的距离是巨大的,并且m是常数。现在分别按照(d2i/dx2+d2i/dy2)是正的或负的,视网膜部位感觉到自身比在用符合于其自身的强度均匀照亮相邻部位时更暗或更亮。如果表面f(x,y)具有边与凹入处,则(d2i/dx2+d2i/dy2)变为无穷的,并且这个公式不能使用了。在这个场合,对应于凹入处的当然是一种强烈的发暗或发亮,而决不是无穷的发暗或发亮。发暗与发亮也决没有严格的界线,而是象按照偏离开平均值的大小必然会预期到的那样,交错在一起进行的。视网膜并不是由各个感觉点构成的,而是由数量有限、规模有限的感觉要素构成的。现在还缺乏关于这些要素的相互作用规律的详细知识,它似乎对于更精确地规定这个特殊场合的现象是必不可少的。
既然我们在按照主观印象去判断光的客观分布时可能容易出错,所以上述对比规律的知识甚至于对纯粹物理学研究也有重要意义。格里马尔底(Grimaldi)就曾经由于这样一种现象而有过错觉。我们在考察阴影、光谱吸收以及其他无数场合,也遇到了同样的现象。由于一些特殊的情况,我的有关这个问题的报导没有得到广泛传播,并且在三十多年以后又第二次发现了这些有关的事实。
能够引人注目的事实是:除了i以外,还有i的二阶微分系数,而不是一阶微分系数di/dx,di/dy,似乎对亮度感觉发生了一种影响。表面照亮强度的均匀连续提高,例如在x方向上,我们几乎察觉不出来,而要确信有这样的提高过程,就必需有一些特别的仪表装置。反之,这些一阶微分系数则对所视表面的模拟、塑造表现出了它们的影响。如果我们称水平方向为x,称所照表面上一个点的深度距离为T,则di/dx与d2τ/dx2是平行的。这种当然又只能在象征意义上理解的表达式说明,一个具有垂直母线与平面水平准线的圆柱表面向我们表现为τ=F(x),它的二阶微分系数d2τ/dx2(曲率)平行于表示照亮强度的一阶微分系数(陡度)。曲率的规迹取决于第172页上指出的配连条件。
关于单眼映象引起的深度感觉,下列实验是有教益的。图28是一个有两条对角线的平面四角形。我们用单眼看这个图形,它按照概率原理与经济原理,最容易表现为平面的。不平的对象在极大多数场合强制眼睛去观看深度。在没有这种强制的地方,平面对象是最可能的对象,同时对于现觉器官也是最惬意的对象。
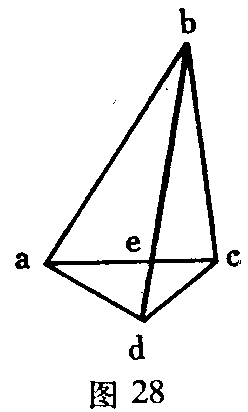
这同一个图形在单眼中还可以看作一个其边bd在ac之前的四面体,或看作一个其边bd在ac之后的四面体。表象与意志对视觉过程的影响是极其有限的,仅限于注意力的引导,限于视觉器官的气质对这器官所习惯的许多场合中的一种场合的选择,而其中每个选择的场合都以刻板的可靠性与准确性确定其位置。我们在注视点e的时候,实际上可以按照我们把bd想象得比ac更近或更远,而随意地更换这两种在视觉上可能的四面体。对于这两种场合,视觉器官都有影响,因为一个物体往往部分地为另一物体掩盖起来。
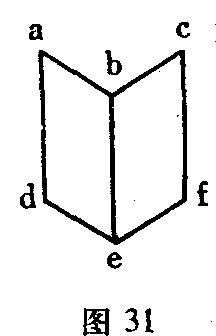
勒卜发现,眼睛靠近图31,引起了对于近距离的调视,从而也引起了把固定边be看成是突起来的这个结果。我未能得出这样肯定的结论,也未能从理论上找到说明这个结论的充分理由,虽然我乐于承认图形距离的改变容易导致我们对图形的看法的变化。

最后,如果把划出的交点e想象为处于平面abcd之前或之后,这同一个图形则可看作是一个四边梭锥体。如果bed和aec是两条完全的直线,则难以做到这一点,因为要把直线毫不勉强地视为打折的,这与视觉器官的习惯有冲突;只有点e有一个引人注目的部位,这一做法才能成功。但如果在e处有一个很小的压痕,则这一实验没有什么困难。
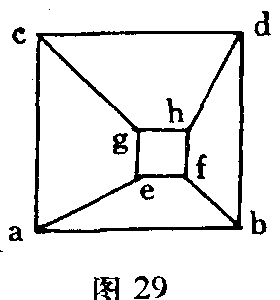
对透视毫无知识的人,一俟他象在用单眼作观察时容易做到的那样,能完全不考虑图形的平面,就会象具有完备的透视理论知识一样,确实看到直线透视图形对他的影响。按照我的信念,对所视对象的思考、甚至回忆都很少涉及或全不涉及这种影响。图形中的直线为什么看起来是空间中的直线,这是已经研讨过的问题。当各条直线似乎在图形平面的一个点上收敛时,各个收敛的或逼近的终端就会按照概率原理和经济原理,而被移动到同样的或几乎同样的深度。这样就给出了没影点的效果。这样一些直线可能看起来是平行的,但并不存在造成这样一种印象的必然性。如果我们用眼在同样高度上看图29,它就能给我们显示出向一个通道深处看的景象。终端ghef被移动到了同样远的地方。如果距离很大,则在这里直线ae、bf、cg与dh显得是水平的。如果把这个图形抬高,则终端efgh升高,而底部abef似乎有向上的坡度。在把图形放低时,则出现相反的现象。我们向右侧或左侧移动图形,也会看到类似的变化。在这里透视作卷第97页)指出了调视对深度视觉的意义很小。用的各个原理得到了简明扼要的表达。
平面图形如果完全是由到处都正交的直线构成的,则显得几乎总是平面的。如果出现了斜交与曲线,则如图30所示,容易从平面里突现出一些线,我们可以毫不费力地把它们理解为曲页。如果象图30这样一个轮廓在空间中采取一定形式,并且我们把它视为一个表面的边界,则简言之,这个表面显得尽可能平坦,因此又显得偏离深度感觉的平均值最小。
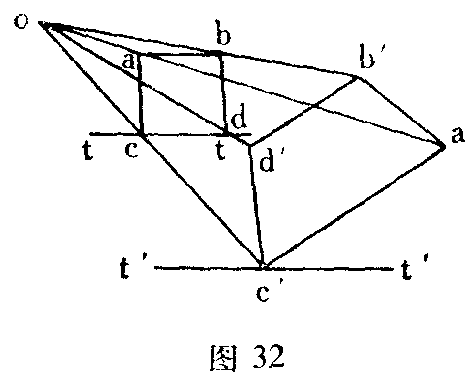
那些在图形平面(或者在视网膜)上斜交的,因而彼此从图形平面(或者从垂直于视线的平面)突出的线,具有一种独特的相互作用,对于这种相互作用,我第一次借助于上述(第171页)名片单眼反演实验的机会作了观察。图31中的纸片向我凸出的边be处于垂直位置,当我能象把书放到桌上那样,看见be 是凹入时,纸片就放倒了,以致b显得比e更远。如果我们有朝一日熟悉了这种现象,那么,我们几乎在任何对象上都能做出反演,而且后来我们总是能够随着形式的改变(翻转)而同时观察到客体方向(位置)的那种奇特的改变。特别令人诧异的是在透明对象那里形成了一种变化过程。假定abcd是桌子tt上的一个玻璃骰子的截面,o是眼睛。在单眼反演中,棱角a移向a’,而b紧挨着移向b’,c移向c’,d移向d’。骰子看起来是以其棱角c’叙置于桌子tt上。要更明显地形成这个图形,两个图象就不能彼此交错地加以描绘,而是先后相继地描绘出来的。一个部分地装着有色液体的玻璃酒杯,如果放到了骰子的位置上,当然也会连同其液体表面,有同样的倾斜位置。
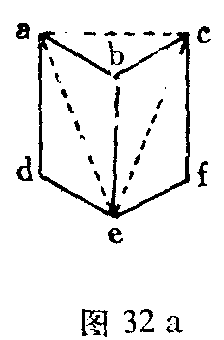
给予足够的注意,我们也会在任何直线图形上观察到这类现象。如果我们把图31中的纸片垂直叠放在我们面前,并且用单眼加以观察,我们就会看到,当be凸出时,b则突起,当be凹入时,e则突起,接近于观察者,并且b后退。勒卜注意到,在这种情况下点a,e仍然在图形的平面上。实际上,这就使方向的变化成为可理解的了。如果我们作三条虚线(图32a),设想这个在虚线三角形之外很远的图形已经消去,在我们这里就会留下一个中空的或突起的三边梭锥体的图象,它的底在图形平面上。反演不再引起任何不可理解的方向变化。因此,事情似乎是这样的:任何单眼所视的点都力求偏离开深度感觉的平均值最少,整个所视对象力求脱离开赫林核心表面的距离最小,而这是在实验条件下可以达到的。
如果我们注意平面直线图在单眼空间解释中所经历的变形,我们则可将这种变形从性质方面归结为下列原理:锐角的两边冲向图形的平面或垂直于视线的平面的两个对边,钝角的两边冲向同一个边。在这种情形下,锐角扩大了,钝角缩小了。一切角都力求变为直角。参看附录15。
这条原理表明,刚才所说的现象同策尔纳讲的幻视术以及其他许多类似现象有关。即使在这里,一切也是归结为锐角在表面上扩大与钝角在表面上缩小,只不过图形在所视平面中有变化。但如果我们靠单眼在空间中看这些图形,则幻视术消失了,接着出现的是以前所描述的那些现象。虽然这类幻视术现在已经从许多方面加以研究,但目前并没有完全令人满意的解释。如果全部探讨并未做出或已经夭折,我们当然不能同意这样草率的解释,例如说什么我们习惯于首先看直角。我们常常看到斜角的对象,而决没有作任何人为的处置,例如在上述实验中,我们就看到静止倾斜的液体平面。不过,眼睛似乎宁愿看到一个斜角的物体有倾斜的液体平面。
我相信,表现于这些过程的基本力量在视觉器官的很简单的习性中有其根源,而这种习性几乎首先不是在人类文化中产生的。我曾经试图用一种类似于颜色对比的方向对比,来解释这些现象,但没有取得一个令人满意的结果。勒卜、亥曼斯等人的新近研究和赫夫勒关于曲率对比的观察,现在却在说法方面很有利于对比理论。至少在最近时期,甚至拥护纯粹生理学解释的倾向也得到了决定性的增长。
经济原理对我来说在策尔纳讲的幻视术方面也显得毫无启发性。对取得成就能提供某种更大的希望的似乎是概率原理。我们设想视网膜是完整的圆球,眼睛在空间里固定在角a的顶点。通过眼睛的中心和角的两边而把这两个边投射到视网膜上的平面,在视网膜上割出一个具有角A的球截形,它代表单眼映象的角。可能对应于同一个任意的A的,现在有a在0度与180度之间的无数的值,象我们考虑对象的角的两边在上述投影平面可能采取任一位置时看到的那样。因此,可能对应于所视角A的是对象的角a的一切值,当我们令三角形边b与c的任何一边在0度与180度之间变化时,这一切值就都得出来了。在这里,假定计算是以一定方式进行的,得出的实际结果就是:对应于所视锐角的是作为最可能的对象的较大的角,对应于所视钝角的是较小的角。然而我不能断定,那些被我们倾向于认为在几何学上同样可能的情况是否也可以视为在生理学上是同样可能的,这个问题也许是本质的与重要的。在我看来,整个考察方式也具有过分人为的性质。
在这里不能不提到,施特尔(A.Stohr)曾经试图从崭新的观点出发获得关于上述现象的解释。对于指引施特尔的一般考虑,我必须完全表示同情与同意。但他的假设是否符合于实际上可以证实的原理,我至今都不可能作出肯定的判断。他所假定的关系也是很复杂的,以致如果不重新就这个领域本身通盘进行实验,就难以对这个问题作出判定。因此,我不知道施特尔的观点是否在一切地方都足以作出解释。他的一部早期著作假定,对应于眼睛在视网膜前的折射映象的是视网膜中的反射映象,反射映象的浮雕与视网膜的深度成比例。视网膜的深度也许同时是视觉空间深度的决定因素和眼睛调视活动的调节因素。实际上,我总是反躬自问,究竟什么东西决定调视活动变化的感觉,因为这种变化不能取决于色散圆圈之单纯大小,收敛与调视之间的联系也仅仅是松散的联系,而一只眼睛也可以是自调的。另一方面,许多观察都与这种观点相对立,说调视对深度感觉失去了价值。昆虫眼睛的视网膜很厚,这又表明浮雕知觉可能与视网膜的某种功能有关。
在他的后来的两部著作中,他以这个观点为基础,进一步作了论述。其中的第二部著作以具有较多的生理学意义的形式,提出了舍夫勒的观点。盛行的观点认为,或多或少偏离开对应部位的部位映象融合为统一的印象,施特尔觉得这种观点是不能令人惬意的。他写道,“什么地方会有一种扳道工,他不仅以非凡的方式,而且也以合乎目的方式安排变比,使一对不熟习的导线轨道能把两个刺激在中枢器官里联合起来呢?”他假定,双眼的视网膜为一种求力达到最小限度的光刺激的活动所支配,因而希望达到不同映象之相等。神经要素刺激睫状肌,其方式不仅是完全均匀的、合乎规则的,而且根据需要,也是很不均匀的。睫状肌之合乎规则的收缩,引起晶状体之更大弯曲和视网膜之微小收缩。在这里如果视网膜要素带有其位置值,则同一视网膜映象就会显得增大。这样,按照施特尔的看法,我们就可以理解,潘诺慕的比例圆圈系统(以至半径比例4:5)之所以被看成简单的与具有平均数的,是由于双眼彼此与同一视网膜部位之适应。施特尔交替地用红点描绘一个圆圈系统,用绿点描绘另一圆圈系统,使得在双眼复象中红点表现于绿点之间,从而证实各个圆圈系统的融合并非由于压迫一个映象所致。睫状肌的不均匀收缩现在被认为引起一些不同的结果:首先是晶状体随着光束折射顶点的各种位移而产生的不规则变形,从而出现折射映象与反射映象的浮雕的变化,其次是视网膜的各种最小限度的变形。施特尔相信详细的计算能说明他的观点的可能性,观察者对缺晶病眼的研究能证实他的前提的真实性。无论如何,他的理论已经引导他做出了令人惊讶的实验,例如,在体视镜中直线的弯曲,因而他的理论值得重视。不过,虽然对于他把眼睛及其各个部分视为活有机体的观点我颇表同情,但我还不能相信他的假定就到处都足以解释很复杂的空间视觉情况。
施特尔同生理光学传统相距甚远。艾克斯纳与毕尔的生理学研究就美好的、值得注意的成果作了充分比较,已经使我们认识到眼睛具有物理学家几乎不可能a priori[先验地〕猜想到的很复杂的有机装置,从这时起就压根儿不可能有什么理由,不去准确检验施特尔的理论了。也许施特尔的思想虽然在人的眼睛上得不到应用,但在别的视觉器官上能得到应用。参看附录16。
在看东西的时候眼睛里还有一些需要研究的变化过程,这从许多现象来看是可能的。具有明显体视差别的体视图象,在长期加以注视时,还显示出一个有不断异常增大的浮雕,尽管融合过程似乎早已完成。在精细的、光滑的和平行的直线系统上,有人观察到了波状的弯曲与起伏,并以某种独特的方式,把它们归因于不足以解释这样精细的直线的视网膜嵌合体。但是在能够看得很清楚的、决非微观度量的直线系统上,我加以不断观察,也总是看到这种现象。因此,事情确实与视网膜联合体无关。我宁可相信,通过努力,例如通过施特尔意义上的微小位移,就使空间的量值陷入某种无序状态。
平面图形的幻视容易转化为平面图形的单眼空间视觉,这种情况就很有助于对那种幻视作出进一步的解释。下列事实加强了这个推测。一个平面直线图用单眼来看,通常显得是平面的。但如果我们改变角度,并引入运动,则任何这样的图形都会立刻向深度伸张。这时我们通常看到的是一个正在转动的固体,就象我在以前的一个场合描述过的那样。尽人皆知的利萨如(Lissajous)振荡图在相差变更时,似乎是处在一个转动的圆柱体上,这给上述过程提供了一个很好的例证。
我们在这里可以又指出对待固体的习惯。实际上在我们周围经常有一些正在转动与变向的固体。诚然,我们在其中运动的整个物质世界在某种程度上就是一个固体,找们不借助于固体,一般就得不到几何空间观念。我们通常也不注意物体的各个点在空间中的位置,而是直接把握物体的量纲。在这里对于未经训练的人来说主要是存在着作出透视图的困难。习惯于观看物体的真实大小的儿童,不能理解透视中的尺寸缩短,而更多地满足于简单的正视图和侧面图。我能很清楚地回忆起这种情况,并通过这种回忆理解古代埃及人的图画,这些图画尽可能描绘一切物体部分的真实大小,因而仿佛把这一切部分都压到了图形平面中,就象把植物压为标本一样。甚至在庞培人的墙画上,我们也遇到了一种害怕缩短尺寸的明显痕迹,虽然在这里透视感已经是清楚的。反之,古代意大利人则按照他们的实际了解的感受,而往往沉湎于过度的、有时甚至很不象样的尺寸缩短,这种缩短有时需要眼睛作出相当可观的努力。
因此,毫无问题,观看突出点距离固定的固体对我们来说要比分辨深度熟习得多,而分辨深度总是通过有意的分析才作出的。所以,我们可以预期,凡在感觉群集借助连续过渡与共同颜色特点融合为统一整体,显示空间变化的地方,这种变化都偏向于被看成固体的运动。但我必须承认,这种看法并不令我满意。倒不如说,我相信即使在这里视觉器官的基本习性也是基础,这种习性并不是通过自觉的个人经验产生的,而是相反地减轻了我们把握固体运动的活动。例如,假使我们认为,我们所注意的视觉群集横断量纲的任何缩小都力求引起纵深量纲的相应扩大,或纵深量纲的任何扩大都力求引起横断量纲的相应缩小,那么,这个过程也许就完全类似于我们在上文设想的(第163页)、可以同能量守恒相比的过程。这种观点肯定简单得多,并且同样足以作出解释。而且这也能够使我们更容易设想这样一种基本习性是怎样获得的,它如何在有机体中得到表现,它的性状会怎样加以遗传。
我想在这里再作另一种观察,作为对视觉器官呈现给我们的固体转动的补充。如果我们在桌上转动一颗鸡蛋或表面黯淡均匀的椭体,不过不是绕着转动物体的轴旋转,而是作颠簸运动,我们在用单眼观察时就会相信在我们面前有一种流体,一个大的振动的水滴。如果让长轴在水平面上的鸡蛋绕着垂直轴作适度的迅速转动,这种现象则更其令人注目。如果鸡蛋的表面带有斑点,我们能用眼追踪表面的运动,这种印象就立刻消失了。这时我们看到的就是转动的固体。
本章所作的解释确实还很不完备,但我相信,我的论述会引起和开创关于上述现象的更精确、更深入的研究。
------------------