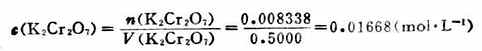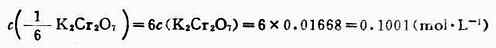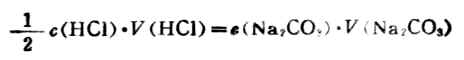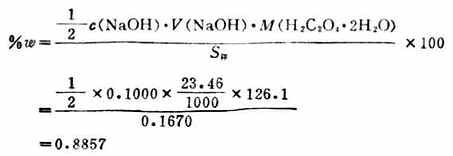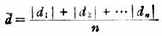|
《医用化学》 > 第七章 滴定分析
第一节 滴定分析概念
一、滴定分析的特点和方法滴定分析是通过“滴定”来实现的一种分析方法。在滴定过程中,使用的已知准确的溶液称为标准溶液,被滴定的溶液叫做试样溶液。当标准溶液与被测组成的反应恰好完全时,即为反应的理论终点,称为化学计量点附近发生的、容易观察到的变化来确定。若反应本身无此种变化,就须借助指示剂。指示剂所指示的反应终点称为滴定终点。 滴定分析法是基于标准溶液与被测组分之间发生化学反应时,它们的量之间存在一定的化学计量关系,利用标准溶液的浓度和所消耗的体积来计算被测物质含量的一种方法。根据分析时所利用的化学反应不同,滴定分析又分为酸碱滴定法,氧化还原滴定法,配合滴定法和沉淀滴定法。 值得注意的是,并非所有的反应都可用于滴定分析,适合滴定分析的反应必须满足以下条件:第一,该反应必须按一定的反应式进行,即必须具有确定的化学计量关系;第二,反应必须能够定量地进行,通常要求达到99.9%以上;第三,必须有适当的方法确定反应的终点。此外要求反应能较快地进行。对于速度较慢的反应有时可通过加热或加入催化剂来加速反应。
二、滴定分析的操作程序(一)标准溶液的配制 1.直接配制法 直接称取一定量的基准物质,溶解后转入容量瓶中,稀释定容。根据溶质的量和溶液的体积可计算出该溶液的准确浓度。 所谓基准物质是指那些能够直接用来配制溶液的物质。它们必须符合下列条件: (1)物质的组成应与化学式相符。若含结晶水,其结晶水的含量也应与化学式相符。 (2)试剂要纯度高。一般含量在99.9%以上。 (3)试剂要稳定。如不易吸收空气中的水分及二氧化碳,不易被空气氧化等。 (4)有比较大的摩尔质量,以减少称量所引起的相对误差。 常用的基准物质有邻酸氢钾、草酸、碳酸钠等。 2.间接配制法 由于大多数试剂不能满足基准物质的条件,也就不能直接用来配制标准溶液。这时可先将它们配成近似所需浓度的溶液,再用下述方法标定其浓度,这种方法称为间接配制法。 (二)标准溶液浓度的标定 标定是指用滴定方法确定溶液准确浓度的过程。可以用待标定溶液一定量的基准浓度,亦可以用待标定溶液和已知准确浓度的标准溶液进行相互滴定,比较出待测溶液的浓度。例如,欲标定盐酸溶液的浓度,可称取一定量的分析纯碳酸钠(基准物质)溶于水中,然后用此盐酸溶液进行滴定: 2HCL+Na2CO3→2NaCL+H2O+CO2 当反应完全时,从用去此盐酸溶液的体积和碳酸钠的质量,即可求出盐酸溶液的准确浓度。 (三)被测物质含量的测定 标准溶液的浓度确定后,即可对待测物质进行含量测定。例如,已标定的盐酸溶液可以用来测定某些碱性物质含量;已标定的氧化剂溶液可以用来测定某些还原性物质相对含量。
三、滴定分析的计算方法(一)方向方法 滴定分析中的计算主要包括标准溶液浓度的计算和被测定物质含量的计算。标准溶液的浓度常用物质的量浓度表示。物质B的浓度即可用下式求得: cB=nB/Vb (7-1) 或 cBVB=mB/MB(7-2) 在上面式子中,mb 为物质B的质量(g);MB 为物质B的摩尔质量(g˙mol-1);VB为物质B溶液的体积(L);cB即为物质B的量浓度(mol˙L-1)。 对于任一滴定反应: aA+bB=dD+eE 若选取aA和bB作为基本单元,则有如下关系: n(aA)=n(bB)(7-3) 上式表示:当达到化学计量点时,aA与bB的物质的量相等,即等物质的量规则。该规则是进行滴定分析计算的主要根据之一,由式(7-1)和式(7-3)得: c(aA)˙V(A)=c(bB)˙V(B) 在实际工作中,为方便起见,常将A和B选作基本单元。
故式(7-4)又可写成:
式(7-2)和(7-5)是滴定分析中两个常用的计算式,下面通过实例介绍它们的应用。 例1 准确称取基准物质K2Cr2O72.4530g,溶解后移入500ml容量瓶中,加水稀释至刻度。求c(K2Cr2O7)和 解:K2Cr2O7的摩尔质量为294.2g.mol-1 故 则
例2 称取分析纯Na2CO31.2738g,溶于水后稀释成250mL,取该溶液25.00mL,用HCl溶液进行滴定,以甲基橙为指示剂。当达终点时,用去HCl溶液24.80mL,求此溶液的准确浓度。 解:滴定反应为 Na2CO3+2HCl→2NaCl+CO2+H2O 由式(7-5)得
因为 所以 在上式中溶液的体积是以升为单位,若体积V指定以毫升为单位,则上式可化为 则 在25.00mL Na2CO3溶液中Na2CO3的质量为: 所以 例3 称取草酸0.1670g溶于适量的水中,用0.1000mol.L-1的NaOH标准溶液滴定,用去23.46mL,求样品中H2C2O4.2H2O的质量百分数。 解:滴定反应为
则草酸的质量百分数:
(二)有效数字和计算规则 有效数字是指实际上能测量到的数值,在该数值中只有最后一位是可疑数字,其余的均为可靠数字。它的实际意义在于有效数字能反映出测量时的准确程度。例如,用最小刻度为0.1cm的直尺量出某物体的长度为11.23cm,显然这个数值的前3位数是准确的,而最后一位数字就不是那么可靠,因为它是测试者估计出来的,这个物体的长度可能是11.24cm,亦可能是11.22cm,测量的结果有±0.01cm的误差。我们把这个数值的前面3位可靠数字和最后一位可疑数字称为有效数字。这个数值就是四位有效数字。 在确定有效数字位数时,特别需要指出的是数字“0”来表示实际测量结果时,它便是有效数字。例如,分析天平称得的物体质量为7.1560g,滴定时滴定管读数为20.05mL,这两个数值中的“0”都是有效数字。在0.006g中的“0”只起到定位作用,不是有效数字。 在计算中常会遇到下列两种情况:一是化学计量关系中的分数和倍数,这些数不是测量所得,它们的有效数字位数可视为无限多位;另一种情况是关于pH、pK和lgK等对数值,其有效数字的位数仅取决于小数部分的位数,因为整数部分只与该真数中的10的方次有关。例如,pH=13.15为两位有效数字,整数部分13不是有效数字。若将其表示成[H+]=7.1×10-14,就可以看出13的作用仅是确定了[H+]在10-14数量级上,其数学意义与确定小数点位置的“0”相同。 在滴定分析中,实验数据的记录只应保留一位可疑数字,结果的计算和数据处理均应按有效数字的计算规则进行。 在进行加减运算时,有效数字取舍以小数点后位数最少的数值为准。例如,0.0231、24.57和1.16832三个数相加,24.57的数值小数点后位数最少,故其他数值也应取小数点后两位,其结果是 0.02+24.57+1.17=25.76 在乘除运算中,应以有效数字最少的为准。例如,0.0231、24.57和1.16832三个数相乘,0.0231的有效数字最少,只有3位,故其他数字也只取3位。运算的结果也保留3位有效数字: 0.0231×24.6×1.17=0.665 在对数运算中,所取对数的位数应与真数的有效数字位数相同。例如,lg9.6的真数有两位有效数字,则对数应为0.98,不应该是0.982或0.9823。又如[H+]为3.0×10-2mol·L-1时,PH应为1.52。 正确运用有效数字规则进行运算,不但能够反映出计算结果的可信程度,而且能大大简化计算过程。在滴定分析中一般常采用四位有效数字。
四、滴定分析的误差(一)误差及其来源 在滴定分析中,分析结果的准确度常用误差来表示。误差是测量值与真实值之间的差异,它反映出分析结果与真实值间的符合程度。努力减少测量误差,提高分析结果的准确性是定量分析中的一项重要课题。 滴定分析中最常见的误差有系统误差和偶然误差。 1.系统误差 系统误差是由某些必然的或经常的原因造成的。其来源有方法误差,仪器、试剂误差及操作误差等。系统误差对分析结果的影响有一定的规律性,在重复测量时误差的大小常常比较接近,并且会反复出现。与理论值相比,实验值要么都提高,要么都偏低。系统误差常用作空白试验和对照实验的方法消除或克服。 在不加试样的情况下,按照样品分析步骤和条件进行分析试验称为空白试验,所得结果称为空白值。从试样测定结果中扣除空白值,便可以消除因试剂、蒸馏水及实验仪器等因素引起的系统误差。 将组分含量已知的标准样品和待测样品在相同条件下进行分析测定。用标准样品的测定值与其真实值的差值来校正其他测量结果,这种方法称为对照试验。 除此之外,还可以通过校准仪器来消除仪器误差,通过制订正确的操作规程克服操作误差。 2.偶然误差 偶然误差是由一系列微小变化的偶然原因造成的。例如,称量同一物体时,室温或湿度如有微小变动都会引起偶然误差,使得称量结果不一致。这种误差大小不定,时正时负,往往找不出确定的原因,因些很难控制、校正和测定它。但偶然误差符合统计规律,表现为正负误差出现的机会相等,小误差出现的机会多而大误差出现的机会少。因此,在消除了系统误差的前提下,可以通过增加测定次数取平均值的办法克服偶然误差。 (二)误差与准确度 准确度指实验测定值(X)与真实值(T)之间的符合程度,常用误差的大小来衡量。误差的绝对误差和相对误差。绝对误差指测定值与真实值之间的差值,用“E”来表示。相对误差指的是绝对误差占真实值的百分率,用“%RE”表示。即 绝对误差:E=X-T 相对误差:(%)RE=E/T×100 误差越小,表示实验结果与真实值越接近,测定的准确度也越高。而与绝对误差相比,相对误差更能反映出实验结果的准确程度。因此在滴定分析中一般多采用相对误差来表示测量的准确度。 (三)偏差与精密度 在实际工作中真实值往往是不知道的,此时便不好用误差来评价分析结果,通常用相同条件下多次测定结果的平均值(X) 来代替真实值,用偏差来衡量所得结果的精密试。 精密度指多次重复测定的结果相互接近的程度,是保证准确度的前提。偏差是指各次测定的结果和平均值之间的差值。偏差越小,精密度越高。 偏差分为绝对偏差(d)、相对偏差(Rd)、平均偏差(d)和相对平均偏差 (Rd),它们的表达式为: 绝对偏差 相对偏差 平均偏差 相对平均偏差 式中d1,d2…dn为第1,2…n次测量结果的偏差,X为单次测定值,x为测定平均值。 对于一般的滴定分析来讲,因测定次数不多,故常用相对平均偏差来表示实验的精密度。
…… 第六章 氧化还原与电极电位 第一节 氧化还原 第二节 电极电位 第三节 电极电位的应用 第七章 滴定分析 第一节 滴定分析概念(当前页) 第二节 酸碱滴定法 第三节 氧化还原滴定法 第四节 配合滴定法 第八章 比色分析 …… |

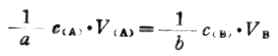
 。
。