感觉的分析
作者: 恩斯特·马赫
第六章 眼睛的空间感觉
树有它那灰色的、坚硬的、粗糙的躯干,有许多在风中摇曳的枝条,有光滑的、发亮的、柔软的叶子,它首先在我们面前表现为单个的、不可分离的整体。同样,甜的、圆的、黄色的果实,光亮的、灼热的、冒着多种多样火舌的火,我们也都认为是单个的物。单个的名称表示整体,单个的词就象在一根线上一样,立刻从深刻的遗忘中引起一切联系起来的记忆。
树、果实或火的映象是可见的,但不是可触知的。当我们的视线转向别处,或我们的眼睛闭上的时候,我们能触知树,品尝果实,感受火焰,但是我们看不见它们。因此,看起来统一的物就分离成各个部分,这些部分不仅相互制约,而且也受其他条件的制约。看得见的东西是与可触知的、可品尝的东西等等分离开的。
单纯可见的东西也是在我们面前首先表现为单个的物。但我们在一朵黄色的、星状的花旁边也能看到一个黄色的、圆的果实。第二个果实可以同第一个果实一样圆,但它是绿色的或红色的。两个物可以颜色相同而形式不相同;它们也可以颜色不同而形式相同。视觉由此而划分成为颜色感觉和空间感觉,尽管这两种感觉不能被描述为各自孤立的,但它们却彼此不同。
我们在这里不作详细探讨的颜色感觉,主要是一种对于有利的或不利的化学生存条件的感觉。在适应这些条件的过程中,也许颜色感觉发展和变化了。光进入有机生命中。绿色的叶绿素和(互补的)红色的血红蛋白在植物躯体的化学过程和动物躯体的化学反映过程中占有重要地位。这两种物质向我们呈现出最多种多样的色泽变化。视紫的发现,摄影和摄影化学的经验,使我们也可以把视觉过程理解为化学过程。颜色在分析化学、光谱分析和结晶学中所起的作用是大家都知道的。这种作用提供了一个想法,即把所谓光的振动不理解为机械的振动,而理解为化学的振动,理解为交替的结合与分离,理解为在摄影化学过程里仅仅朝一个方向加以传导的那种振荡过程。这个观点主要是得到了近来对异常色散所作的研究的支持,符合于光的电磁理论。事实上,在电解的场合,化学也提出了最可理解的电流概念,把电解的两种成分看作是按照相反的方向相互转化的。所以,在未来的颜色理论里,许多生物学-心理学的和化学-物理学的线索可能都会汇合到一起。
由颜色表现出来的对化学生存条件的适应,较之由味觉和嗅觉表现出来的对化学生存条件的适应,需要更大范围的运动能力。至少就这里探讨的、唯独我们能作出直接可靠判断的人类来说,情况是如此。因此,空间感觉(一种机械因素)与颜色感觉(一种化学因素)的密切联系就成了可以理解的。我们现在要进行对视觉的空间感觉的分析。
如果我们观察两个虽然相同但颜色不同的形状,例如两个虽然相同但颜色不同的字母,我们就会一眼看出,虽然它们的颜色感觉不同,但它们的形式是相同的。所以,这些视知觉也一定包含着一些相同的感觉成分,而这些成分正是(在两个场合中相同的)空间感觉。
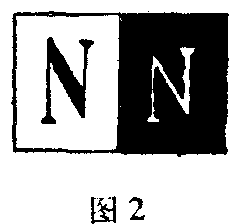
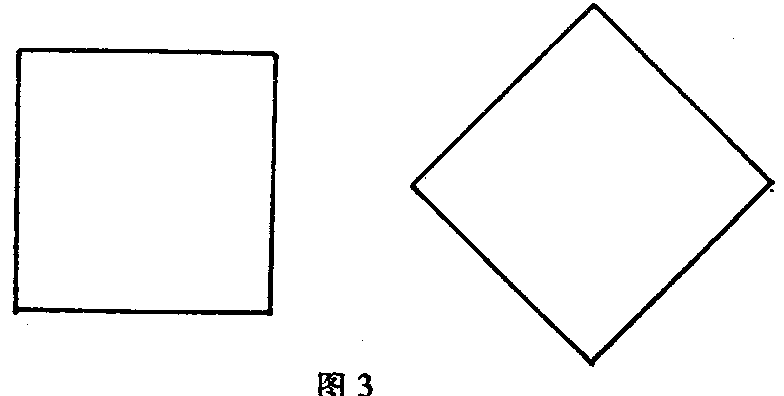
现在我们想研究空间感觉有哪些在生理学上决定图形辨认的性质。首先,这种辨认显然不是出于几何学的考虑,因为几何学的考虑不是感觉的事情,而是理智的事情。倒不如说,我们这里所述的空间感觉可以作为一切几何学的起点和基础。两个图形可以在几何学上是全同的,但在生理学上则迥然不同,如这两个相邻的正方形所表示的,它们如果不经过机械的或心智的运算,就决不可能被认为是相同的。为了熟习这里包含的关系,我们作若干很简单的试验。我们考察的是一个完全任意的斑点(图4)。

如果我们在一条线上按相同方向把这个斑点排列两次或多次,这便会造成一种独特的悦目的印象,而我们也不难一眼看出所有图形都相同(图5)。但如果我们使一个斑点对另一个斑点作大幅度旋转,则除非借助于理智手段,便不再能认出形式的相同(图6)。另一方面,如果我们在涉及观察者的中央平面方面把一个斑点同另一个对称排列起来,则两个形式的明显相似也可以察觉出来(图7)。
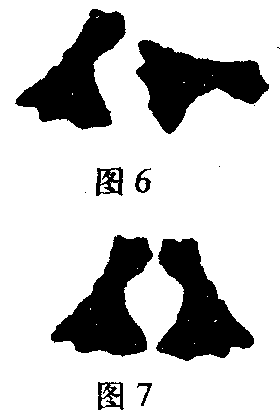
但是,如果对称平面象图8所示,偏离开观察者的中央平面很大,则只有通过旋转图形或心智运算,才能看出形式的相似。反之,如果把一个在自己的平面上旋转了180度的斑点同另一个相同的斑点加以排比,则形式的相似又可以察觉出来(图9)。这样,就产生了所谓的中心对称。
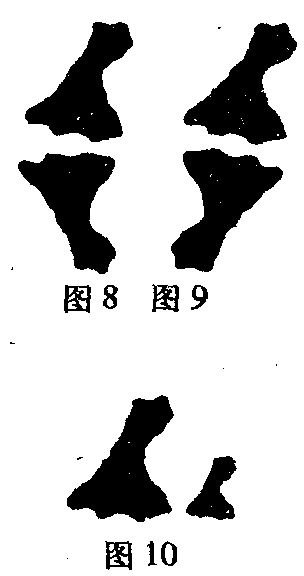
如果我们按同样的比例缩小这个斑点的一切尺度,我们得到的就是一个几何学上相似的斑点。但正象几何学的全同并不是生理学的(视觉的)全同,几何学的对称并不是视觉的对称一样,几何学的相似也不是视觉的相似。只有几何学上相似的斑点同另一个斑点处于同一方向,两者也才在视觉上表现为相似的(图10)。一个斑点的旋转又消除了这种相似(图11)。如果代替这个斑点的是在涉及观察者的中央平面方面对称的斑点,则会产生一种也有视觉量值的对称相似(图12)。一个图形在自己的平面上旋转180度,产生出中心对称的相似,这也具有生理学视觉的量值(图13)。

视觉上的相似与几何学的相似对比,其本质在哪里呢?在几何学上相似的图形里,一切对应线段都是成比例的。但这却是理智的事实,而不是感觉的事实。把具有a,b,c边的三角形同另一个具有2a,2b,2c边的三角形作对比,这种简单的关系并不是直接认出来的,而是应用理智,通过测量才认出来的。如果这种相似也要在视觉上表现出来,那就必须再附加上准确的方向。把具有a,b,c边的三角形与具有a+m,b+m,c+m边的三角形作比较,就可以看到,这两个对象的简单关系对于理智也并不造成一种感觉的相似。两个三角形看起来决不彼此相似。同样,一切圆锥曲线虽然都有一种简单的几何学的相似关系,但看起来却彼此不相似,而三阶曲线则彼此更少显示出视觉的相似,如此等等。
两个图形在几何学上的相似,取决于一切对应线段都成比例,或者说,取决于一切对应角都相等。两个图形只有在位置上也相似,因而一切对应方向都是平行的,或者象我们喜欢说的,都是相同的,才成为在视觉上相似的(图14)。方向对感觉的重要性已经在图3的精心考察中作过说明。所以,正是方向的相同决定了相同的空间感觉,这种感觉标志着形状在生理学视觉上的相似。
被考察的直线或曲线元素的方向在生理学上的重要性,我们还可以用下列考察来说明。假定y=f(X)是平面曲线方程。粗略一望,我们就能看出dy/dx的各个值在曲线上的变化过程,因为这些值取决于曲线陡度;就是关于d2y/dx2的各个值,我们的眼睛也提供了定性启示,因为这些值以曲线曲率为表征。这里显然有一个问题,即我们关于d3y/dx3、d4y/dx4等等的值为什么不能同样直接作出某种陈述?答案很简单。我们看到的当然不是作为理智事实的微分系数,而是曲线元素的方向和一个元素方向对另一个元素方向的偏离。
既然我们直接看出了位置相似的图形是相似的,而且能直接把一个全等的特例与另一个全等的特例区别开,所以,我们的空间感觉就给我们提供了关于方向相同或不相同、量度相等或不相等的启示。
空间感觉无论如何与眼睛的运动装置有联系,这本来就是极其可能的。不必再去详细探讨,我们就首先可以看到,整个眼睛装置、尤其是运动装置,在涉及头部的中央平面方面是对称的。因此,相同的或几乎相同的空间感觉也会与对称的视觉运动相连系。儿童经常把字母b与d、p与q混淆起来。就连成年人也不容易注意到从右到左的转向,除非一些特殊的感性支点或理智支点使他察觉这种转向。眼睛的运动装置具有很完全的对称性。但对眼睛的对称器官的相同刺激本身,却几乎使分辨左右成为不可能的。人的整个躯体、尤其是大脑则只有很少的对称性,例如,这就导致一只手(通常是右手)在运动功能方面居于优势地位。这又导致右侧运动功能的进一步的和更好的发展,导致所属感觉的变化。如果眼睛的空间感觉已经通过书写活动而与右手的运动感觉结合起来,那么,就不再会出现混淆书写技艺与书写习惯涉及的那些垂直对称图形的现象了。这种结合可能变得甚至很坚强,以致各种记忆只有沿着习惯的途径发展,例如,人们只有克服极大的困难,才能读出映现出来的文字。但是,在涉及只能引起纯粹视觉(例如装饰)兴趣,而决不能引起运动兴趣的图形方面,却总是依然出现左右混淆。此外,动物也必定会感到左右的明显差别,因为它只有这样,才能在许多重要场合确定方向。细心的观察者很容易说明,那些与对称的运动功能相结合的感觉怎么会相似。例如,当我因为我的右手偶然做一件事,而用左手抓一个微测螺旋或钥匙时,我就会(不顾以前的考虑)定然把它转向相反的方向,这就是说,我因为感觉的相似而把对称运动与习惯运动混淆起来,从而把对称运动弄成了习惯运动。海登哈恩(Heidenhain)对于半身接受催眠术者的映象文字所做的观察,也属于此列。
左右的区分依赖于对称,而且归根到底还可能依赖于一种化学方面的差别,这是我从我年轻的时候起就有的想法。我已经借着我初次演讲的机会(1861年)说出这个想法。从那时以来,这个想法再三迸发出来。我曾经偶尔从一位老军官那里听说,在昏暗的黑夜,在暴风雪里,在缺少判别方向的外部支点时,军队虽然以为是朝着直线方向行进,实际上接近于在大圆圈上运动,结果几乎又返回到了出发的地点。在托尔斯泰的小说《主人与仆人》里也叙述过类似的现象。这种现象只有用运动的对称性甚小来理解。这种现象类似于一个同圆柱体差不多的圆球在一个更大的圆圈里滚动。关于这类现象,顾尔德贝格(F.O.Guldberg)用迷失方向的人和动物作过深入的研究,他实际上是如此理解这件事实的。迷失方向的人和动物都毫无例外地几乎在一些圆圈里运动,这些圆圈的半径是随物种的不同而变化的,但圆心则分别随着个体与物种的不同,时而在沿着圆圈道路跑动的个体的右侧,时而在它的左侧。顾尔德贝格在这里也看到一种目的论的机制,它可以帮助亲代又找到其失去的饥饿子代。因此,对缺少这个因素的低等动物所作的实验也许是有趣的。此外,根据普遍可能的理由,我们也可望在低等动物那里发现不完全的对称。
勒卜的研究著作《论手的感觉空间》也特别告诉我们一个结果,即右手(在用绷带包起眼睛的情况下)所做的特定运动,如果用左手加以摹仿,则会分别按照个体的不同,而经常被再现为放大的或缩小的。勒卜以为,可以从再生现象得出结论说,左右的差别是一种特殊的差别。但我能担保,我决没有把这种差别视为一种单纯几何学的、量上运动的差别。
象最寻常的经验所述的,根本不同的空间感觉同向上看与向下看有连系。这也是可以理解的,因为眼睛的运动装置在涉及水平平面方面并不对称。重力的方向也对身体的其他运动装置具有莫大的决定作用和重要意义,因而这种情况也必定在服务于其他运动装置的眼睛装置里有其表现。大家知道,一处风景与其在水中的映象的对称性根本无法加以感觉。一位熟人的肖像被上下颠倒,对于不以理智为基准而去识别他的任何人来说,都是陌生的和难以捉摸的。如果我们伫立在一个躺在睡椅上的人的脑后,不假思索,全神贯注于其面部的印象(尤其是在此人说话时),这种印象就是一种完全异样的印象。字母b与p以及d与q,连儿童也不会弄混淆。
以上我们关于对称、相似等等所作的说明,当然不仅对平面图形有效,而且也对立体图形有效。因此,关于深度的空间感觉,我们还需要加以说明。向远看与向近看引起不同的感觉。它们也不应当加以混淆,因为远近之别对人和动物太重要了。它们不可能加以混淆,因为眼睛的运动装置在涉及那种与前后方向垂直的平面方面是不对称的。一个熟人的半身雕塑像不能用其模型来代替,这个经验完全类似于考察上下颠倒所得到的结果。
如果相同的度量和相同的方向引起了相同的空间感觉,同头部中央平面对称的方向引起了相似的空间感觉,那么,这就使上述事实更好理解了。直线在它的一切元素中都具有同一方向,并到处引起同一类空间感觉。它的美感的优越性就在这里。此外,处于中央平面的或垂直于中央平面的直线还以独特的方式表现出来,因为它在这种对称位置上与视觉装置的两半部分有同样的关系。直线的任何其他位置则被觉得是一种“倾斜位置”,是一种对于对称位置的偏离。
同一个空间图形在相同方向上的重复,引起同一空间感觉的重复。各个突出的(明显的)对称点的一切联结线都有相同的方向,并引起同样的感觉。就是把各个单纯几何学上相似的图形在相同方向上并排起来,它们也保持着这样的关系。只不过量度的相等不存在了。但在打乱方向时,这种关系也就打乱了,因而统一的(美感)印象也打乱了。
在一个相对于中央平面的对称图形上,代替相同的空间感觉的是对应于对称方向的相似的空间感觉。图形右半部分对视觉装置右半部分的关系与图形左半部分对视觉装置左半部分的关系是一样的。去掉量度的相等,也仍然感觉到对称的相似。对称平面的倾斜位置打乱了整个的关系。
如果把一个图形与一个旋转了180度的同样的图形并列起来,则会产生中心对称。这就是说,把两对对应点联结起来,联结线则在对应点的一切联结线所通过的一个等分点0相交。就是在中心对应的场合,一切对应的联结线也都方向相同,而这会产生悦目的感觉。失去量度的相等,也依然给感觉留有中心对称的相似。
规则性与对称性相比,显得不具有任何独特的生理学的量值。倒不如说,规则性的量值也许仅仅在于其多方面的对称性,而这种对称性并不单纯是在一个位置上可以察觉出来的。
浏览一遍欧文·琼斯(Owen Jones)的著作(《装饰文典》,伦敦1865年),就会很明显地看到我们作出的论述的正确性。几乎在此书的每个图表中,都会又看到对称的各种类型,作为我们业已获得的观点的佐证。装饰术象纯粹的乐器一样,并不追逐任何附带的目的,而是仅仅服务于人们对形式(和颜色)的快感的,它给我们当前的研究提供了绝妙的事实。支配书写的思想不同于美的考虑。例如,在二十四个大写拉丁语字母里,我们看到有十个是垂直对称的(A,H,I,M,O,T,V,W,X,Y),五个水平对称(E,C,D,B,K),三个中心对称(N,S,Z),而只有六个不对称(F,G,L,P,Q,R)。
原始艺术发展史研究对我们正在讨论的问题是颇有教益的。这种艺术的性质取决于加以摹仿的自然对象、机械技巧的熟练程度以及使用各种重复的形式的努力。
这里所说的事实的美感意义,我已经在以前的著作里作过扼要说明。详细论述这一点,不在我的计划之内。然而我不能不提到,日内瓦的已故物理学家苏雷特(J.L.Soret)在1892年发表的一部很好的书里作过这样的论述,他1866年在瑞士自然科学家协会上所作的一篇演讲应视为这本书的先导。苏雷特继承了赫尔姆霍茨的观点,而似乎对我的论述并不熟悉。这个问题的生理学方面他并未进一步加以探讨,不过,他关于美学方面的论述则颇为丰富,并用引人入胜的事例作为佐证。他考察了对称、重复、相似和连续的美感效果,他把连续视为重复的一个特例。在他看来,同对称的微小偏离都能够以这类偏离所引入的多样性和与此相关的心智审美快感在相当大的程度上补偿肉体快感的损失。这是用哥特式教堂的装饰与雕塑加以解释的。这种心智快感也可以由有效的(潜在)对称产生出来,而这类对称是人们在对称的人体和其他图形的非对称部位知觉到的。此外,苏雷特不仅把这些考察应用于视觉的场合,而且象我做过的那样,把它们推广到一切领域。他注意到了韵律、音乐、运动、舞蹈、自然美和甚至文学。他对盲人所进行的考察特别有趣,洛桑盲人收容所给他提供了作这类考察的机会。盲人对可触对象上的相同形式的周期重复感到愉悦,拥有对于形式对称的决定性感觉。形式对称所受到的显著干扰会使他们感到不快,有时似乎对他们是奇怪的。一个研究过大型欧洲立体地图的盲人,在遇到这个地图按缩小的比例尺构成一个更大的立体地图的组成部分时,仍会借助于几何学的相似,而认出这个大陆来。对称的触觉器官,即双臂与双手,确实安排得类似于视觉器官。因此,这种一致不可能使我们感到惊奇。这种一致已经对古代的研究家有过影响,更不要说对近代的研究家(笛卡尔)了,而且它还产生了一些不幸的观念,它们有一部分现在还在发挥作用。苏雷特书里论述文学的那一章看来不怎么成功。诚然,如我们在以前讨论过的领域里那样,相似的现象表现在韵律、节奏等等上。但是,举例说,苏雷特把莫里哀著名戏剧中重复六次的用语“那个恶魔哺乳,他在这个大木船上做活”的效果与装饰动机的重复相提并论,则不会得到什么赞同。这里的重复肯定不是作为重复产生效果的,而是通过喜剧对立的不断加强,仅仅在心智方面产生了效果。
我还想在这里提请大家注意后来发表的阿诺德·埃姆希(Arnold Emch)的论文《美感形式的数学原理》(载《一元论者》1900年10月号)。他提出一些引人入胜的事例,在这些事例里,一系列形式遵照同一条几何学原理,共同产生了一种美感印象。他遵循了我在我的1871年演讲中提到的思想,即一种按照固定规则进行的生产活动具有美感效果(《通俗科学演讲集》,莱比锡,第三版,1903年,第102页)。但我也曾经同时强调指出,并且现在还想强调指出,规则作为理智的事情本身绝无美感效果,反之,只有由规则决定的同一个感性动机的重复才有这种效果。
在这里应该再次强调指出,必须严格区别空间图形的几何学特性与生理学特性。生理学特性是由几何学特性参与规定的,而不是由几何学特性单独规定的。另一方面,生理学特性很可能曾经给予几何学研究以最初的推动。直线之所以引人注目,并不是因为它是两点之间的最短线段这个特性,而首先是因为它有生理学的单纯性。连平面也是除了它的几何学特性以外,还有一种特殊的生理学视觉的(美感的)量值,这种量值使得平面就象我们还要论述的那样引人注目。按照直角分割平面和空间,这不仅具有由此产生的各部分相等的优越性,而且还有一种特殊的对称量值。全同的或相似的几何图形可以排成一个能在生理学上注意到它们的相似性的方向,这种情形无疑造成了一个结果,即这些类型的几何学相似性较之不怎么引人注目的几何学相似性,诸如仿射性、共线性等等,更早地得到研究。没有感性直观与理智的合作,科学的几何学是不可思议的。而且汉克尔(H.Hankel)也在其《数学史》(莱比锡1874年)中作过精彩的论述,说在希腊几何学中理智因素有决定性的意义,而在印度几何学中则是感性因素有决定性的意义。印度人一般应用对称与相似的原理(参见汉克尔这本书的第205页),而这对希腊人是完全陌生的。汉克尔建议把希腊方法的精确性与印度方法的直线性结合为一种新的表达方式,这是颇为值得记取的。进一步说,我们在这样做时,需要仅仅踏着牛顿与贝努利的足迹行进,这两个人甚至在力学里也都很普遍地应用过相似性原理。对称原理在力学领域里显示出什么优点,我已在另一地方作过详细论述。
------------------